6 La relation CO2 - Température
6.1 L’approche du GIEC
Le GIEC utilise une formule semi-empirique pour lier le forcing radiatif à la teneur en CO2, mentionnée dans (Myhre et al. 1998).
\[ \Delta F=5.35\log (\frac C{C_0}) \tag{6.1}\]
Dans cette formule
| \(\Delta F\) | représente la variation du forcing radiatif, |
| \(C\) | la concentration en CO2 atmosphérique et |
| \(C_0\) | un taux de référence. |
C’est sur cette base que le GIEC prétend que les émissions anthropiques de CO2 provoquent une augmentation du taux de CO2 atmosphérique qui conduit à une augmentation du forcing radiatif qui fait augmenter la température. Mais remarquons au passage que cette expression empirique ne donne pas la direction du lien de cause à effet
Rappelons que le forcing est lié à la température, par un terme analogue à une boucle de rétroaction modifiant l’intensité solaire incidente:
\[ \Delta T= \frac{\lambda _0}{1-\sum f_i} \Delta R_f \tag{6.2}\]
Dans cette expression :
| \(\Delta T\) | représente la variation de la température à l’équilibre |
| \(\lambda_0\) | est une constante [0.32°K/(W/m²)] |
| \(\Delta R_f\) | est le forcing radiatif dû à un doublement du CO2, supposé constant et égal à 4 W/m² |
| \(f_i\) | est la fraction de changement de température dû au mécanisme de feedback i (il s’agit en fait de boutons d’ajustement du modèle) |
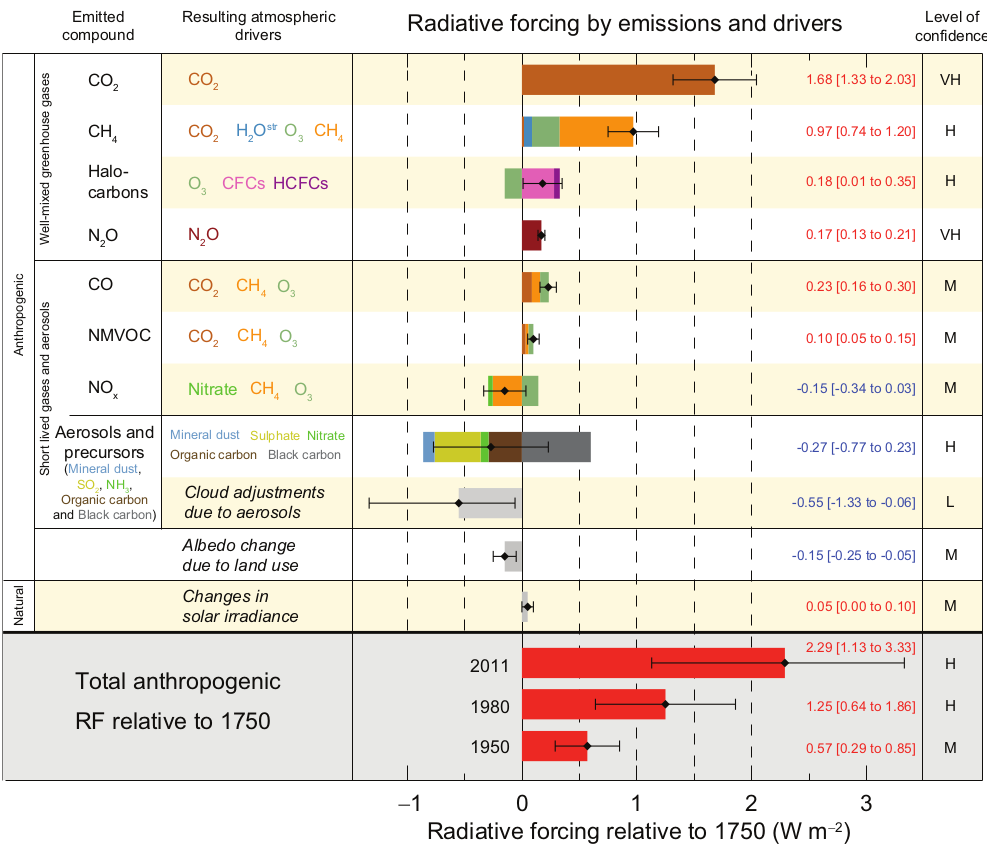
Les autres facteurs climatiques (vapeur d’eau, nuages, aérosols, etc.) apparaissent comme d’autres termes de rétroaction additionnels à l’effet du CO2, rétroactions dont seule la somme entre en jeu. Tous les forcings pris en compte par le GIEC sont repris dans la Figure 6.1.
La valeur exacte de la somme des forcings fait débat, notamment parce qu’elle est susceptible de varier dans le temps et l’espace. Elle se situe quelque part entre 0.4 et 0.75 pour le GIEC, beaucoup moins pour d’autres auteurs.
Certains forcings sont positifs, d’autres négatifs (les nuages par exemple). Cela veut dire que si un forcing négatif (par exemple celui des nuages, qui est très mal connu) est surestimé, le forcing du CO2 sera automatiquement surestimé pour donner le résultat net de rétroaction décrivant au mieux les données expérimentales, mais surestimant les projections faites avec une concentration de CO2 atmosphérique qui augmente.
Il convient enfin de souligner les hypothèses sous-jacentes au concept de forcing, aucune de celles-ci n’étant réaliste:
Les forcings correspondent à une rétroaction dépendant linéairement de la température
Les divers forcings sont indépendants les uns des autres ; leur effet combiné est purement additif
Ils sont instantanés (alors que la Nature comprend de nombreuses constantes de temps, liées à l’inertie des océans, au temps de fonte des glaciers, à la période d’induction saisonnière de la photosynthèse, etc.)
Ils demeurent constants en fonction du temps (négligeant donc, par exemple, les fluctuations de l’intensité solaire et de la couverture nuageuse).
Quelques considérations de chimie-physique et de physique élémentaires permettent d’éclairer le débat.
6.2 Loi de Henry et relation de van ’t Hoff
En recourant à la loi de Henry qui décrit l’équilibre gaz-liquide, et à la relation de van ‘t Hoff qui tient compte de la température, on peut obtenir une formule théorique cette fois, qui est analogue à l’ Équation 6.1.
La concentration océanique de CO2 est liée à la pression partielle du CO2 dans l’atmosphère par la loi de Henry
\[ \mathit{CO}_2^{\mathit{ocean}}(T)=H(T)\mathit{pCO}_2^{\mathit{atm}}(T) \tag{6.3}\]
et donc
\[ \mathit{pCO}_2^{\mathit{atm}}(T)=\frac{\mathit{CO}_2^{\mathit{ocean}}(T)}{H(T)} \tag{6.4}\]
Dans ces formules
| \(pCO_2\) | désigne la pression partielle du CO2 dans l’atmosphère, |
| \(CO_2^{ocean}\) | la concentration en CO2 des océans, |
| \(H(T)\) | est un coefficient (la constante de Henry) qui dépend de la température |
La dépendance à la température de la constante de Henry peut être évaluée par la relation de van ’t Hoff :
\[ \frac{H(T)}{H(T_0)}=\operatorname{e}^{[\frac{\Delta H} R(\frac 1 T-\frac 1{T_0})]} \tag{6.5}\]
Dans cette formule,
| \(\Delta H\) | désigne l’enthalpie standard de réaction. C’est la chaleur de dissolution / dégazage du CO2 , égale à la différence entre les potentiels chimiques du CO2 dissous et gazeux. |
| \(R\) | est la constante des gaz parfaits |
| \(T_0\) | représente une température arbitraire de référence |
Cette formule est valable pour autant que les températures \(T\) et \(T_0\) ne soient pas trop différentes et que par conséquent \(\Delta H\) puisse être considérée constante.
En utilisant l’ Équation 6.4 pour les températures \(T\) et \(T_0\) , et en considérant que la pression partielle du CO2 atmosphérique est proportionnelle à sa concentration, on obtient
\[ \frac{\mathit{pCO}_2^{\mathit{atm}}(T)}{\mathit{pCO2}^{\mathit{atm}}(T_0)}=\frac{k\mathit{CO}_2^{\mathit{atm}}(T)}{k\mathit{CO}_2^{\mathit{atm}}(T_0)}=\frac{\mathit{CO}_2^{\mathit{atm}}(T)}{\mathit{CO}_2^{\mathit{atm}}(T_0)}=\frac{\mathit{CO}_2^{\mathit{ocean}}(T)}{\mathit{CO}_2^{\mathit{ocean}}(T_0)}\frac{H(T_0)}{H(T)} \tag{6.6}\]
Comme la quantité de CO2 dans les océans est très grande par rapport à celle de l’atmosphère, on peut considérer que
\[ \frac{\mathit{CO}_2^{\mathit{ocean}}(T)}{\mathit{CO}_2^{\mathit{ocean}}(T_0)} {\simeq} 1 \]
L’Équation 6.6 se simplifie
\[ \frac{\mathit{CO}_2^{\mathit{atm}}(T)}{\mathit{CO2}^{\mathit{atm}}(T_0)}=\frac{H(T_0)}{H(T)} \tag{6.7}\]
Et en utilisant l’Équation 6.5, il vient
\[ \frac{\mathit{CO}_2^{\mathit{atm}}(T)}{\mathit{CO2}^{\mathit{atm}}(T_0)}=\operatorname{e}^{[\frac{\Delta H} R(\frac 1{T_0}-\frac 1 T)]} \tag{6.8}\]
Soit encore
\[ \log [\frac{\mathit{CO}_2^{\mathit{atm}}(T)}{\mathit{CO2}^{\mathit{atm}}(T_0)}]=[\frac{\Delta H} R(\frac 1{T_0}-\frac 1 T)] \tag{6.9}\]
En exprimant la température sous la forme d’une température de référence et d’une anomalie
\[ T=T_{\mathit{ref}}+\Delta T \tag{6.10}\]
\(\Delta T\) étant faible par rapport à \(T_{ref}\), on peut considérer que \(\frac 1 T {\simeq} \frac 1{T_{\mathit{ref}}}(1-\frac{\Delta T}{T_{\mathit{ref}}})\)
et l’Équation 6.8 devient
\[ \log [\frac{\mathit{CO}_2^{\mathit{atm}}(T)}{\mathit{CO2}^{\mathit{atm}}(T_0)}]=[\frac{\Delta H} R(\frac 1{T_0}-\frac 1{T_{\mathit{ref}}}+\frac 1{T_{\mathit{ref}}}\frac{\Delta T}{T_{\mathit{ref}}})] \tag{6.11}\]
En choisissant
\[ T_0 = T_{ref} \tag{6.12}\]
L’Équation 6.11 s’écrit
\[ \log [\frac{\mathit{CO}_2^{\mathit{atm}}(T)}{\mathit{CO_2}^{\mathit{atm}}(T_{\mathit{ref}})}]=\frac{\Delta H}{RT_{\mathit{ref}}}\frac{\Delta T}{T_{\mathit{ref}}} \tag{6.13}\]
\[ \log [\frac{\mathit{CO}_2^{\mathit{atm}}(T)}{\mathit{CO_2}^{\mathit{atm}}(T_{\mathit{ref}})}]=a\Delta T \tag{6.14}\]
C’est tout à fait équivalent à la formule de Myhre (Équation 6.1).
L’Équation 6.14 peut se mettre sous la forme générique
\[ \log [\mathit{CO}_2^{\mathit{atm}}(T)]=a(\Delta T+b) \tag{6.15}\]
Ou de manière équivalente
\[ \mathit{CO}_2^{\mathit{atm}}(T)\ =\ a\operatorname{e}^{b\Delta T} \tag{6.16}\]
Si l’on pose
\[ L=\log (\mathit{CO}_2^{\mathit{atm}}) \tag{6.17}\]
L’Équation 6.14 peut s’écrire
\[ L(T)-L(T_{\mathit{ref}})=a\Delta T \tag{6.18}\]
C’est l’équation de la dilatation linéaire. La variation du logarithme du taux de CO2 atmosphérique est analogue à la variation de longueur d’une barre soumise à une variation de température.
On peut également faire la comparaison suivante. L’équilibre entre le CO2 océanique et le CO2 atmosphérique est analogue à un système de deux vases communicants dont l’équilibre des teneurs en CO2 dans chaque vase est régi par loi de Henry. Le premier de très grande surface contenant le CO2 océanique, et le second de surface beaucoup plus petite contenant le CO2 atmosphérique. Ajouter du CO2 atmosphérique par des émissions anthropiques, ou en retirer par capture et stockage, dans le compartiment à faible surface n’aura pratiquement aucun effet sur le niveau, lorsqu’un nouvel équilibre sera établi. Il n’y a que la température qui puisse faire changer le niveau d’équilibre, de manière analogue à une dilatation/contraction thermique. C’est cette analogie qui prouve que la variable indépendante (causale) est \(\Delta T\) et non pas le CO2, ce qui contredit l’interprétation de la formule de Myhre faite par le GIEC.
Le même raisonnement peut être tenu pour les autres gaz à « effet de serre » pour lesquels les conclusions précédentes sont également d’application.
Il convient ici de remarquer que :
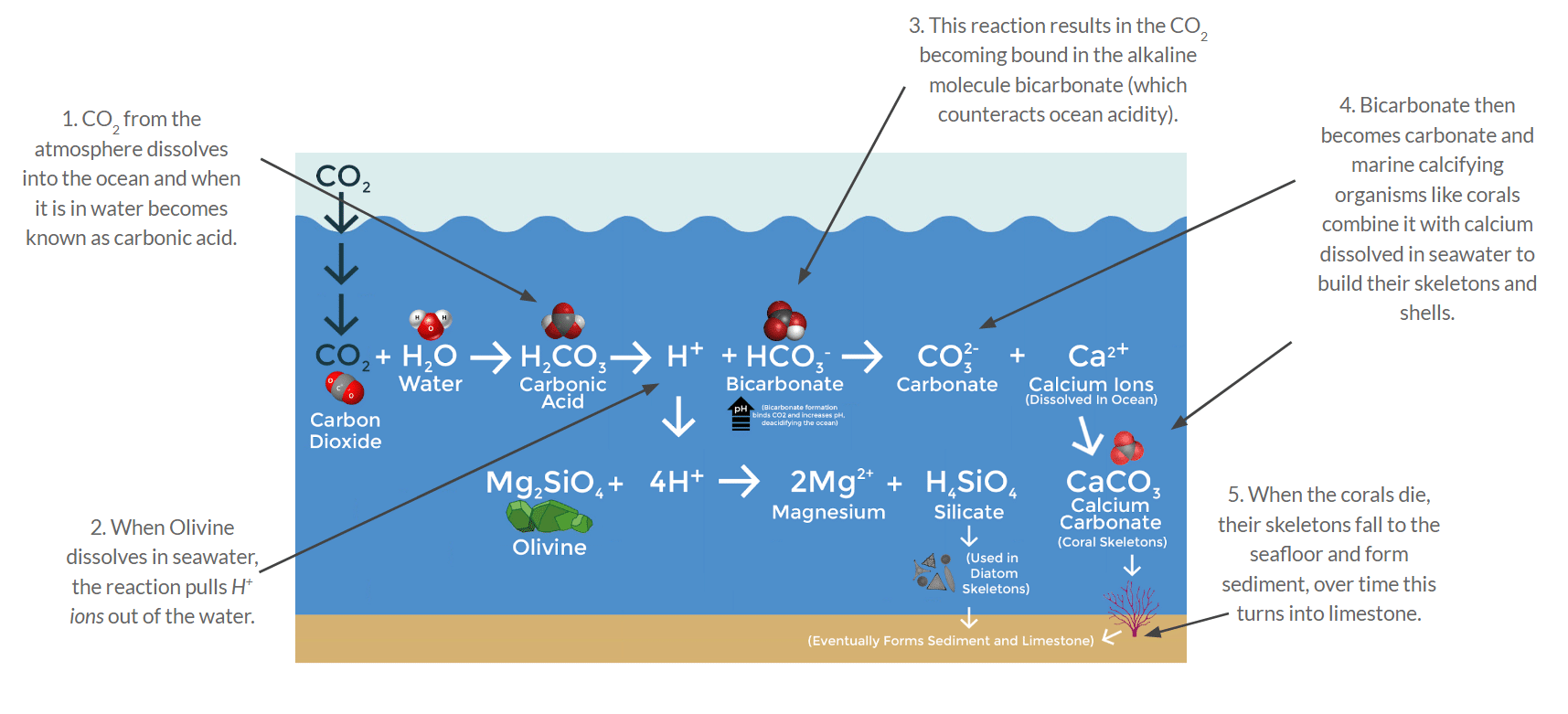
Une bonne partie du CO2 océanique (environ 80%) est fixée sous forme d’ions \(HCO_3^-\) et \(CO_3^{--}=\). C’est l’effet Suess, qui dépend de l’alcalinité, du DIC (dissolved inorganic carbon) et du pH.
L’effet Suess ne tient pas compte des fixations – émissions de CO2 par la biosphère océanique, ni par d’autres équilibres que ceux impliquant les ions carbonates et bicarbonates, tels que les équilibres chimiques concernant les silicates et les phosphates qui interfèrent avec la concentration en ions \(H^+\), et donc stabilisent du moins partiellement le pH (voir Figure 6.2).
Le système océan - atmosphère peut ne pas être à tout instant à l’équilibre.
La chimie carbonatée de l’eau de mer est très compliquée. Une approche simplifiée nécessite la résolution d’un système de 6 équations non linéaires par itérations. Un calculateur en ligne, basé sur un code écrit en langage R, permet d’effectuer ce calcul (« Calculate ocean pCO2 », s. d.). Il y a 3 paramètres en entrée :
l’alcalinité (Titration Alkalinity TA)
la température
le carbone inorganique dissous (DIC)
En modifiant ces paramètres, on obtient en sortie toute une série de propriétés de l’eau de mer dont la salinité, le pH et la pression partielle de CO2 (pCO2).
Si on augmente la température d’un degré, la concentration en CO2 n’augmente que de 11 ppm dans le scénario Preindustrial et de 16 ppm dans le scénario Modern. On pourrait en conclure que l’augmentation de la température ne peut justifier qu’une faible part de l’ augmentation de la pCO2 observée depuis l’époque préindustrielle.
Il faut toutefois remarquer que la pCO2 est égale à 263.5 ppm dans le scénario Preindustrial et passe à 380.7 ppm dans le scénario Modern, alors que la différence de température entre ces deux scénarios n’est que de 1.6 °C. Les 2 autres paramètres (TA et DIC) ont donc un impact très important sur la pCO2 .
On peut constater dans le calculateur que le \(\log (\mathit{CO}_2/\mathit{CO}_2^0)\) que l’on obtient en changeant simultanément les trois paramètres est pratiquement égal à la somme des \(\log (\mathit{CO}_2/\mathit{CO}_2^0)\) calculés en ne faisant varier qu’un seul paramètre à la fois. Voir Table 6.1.
| TA | T | DIC | CO2 | delta CO2 | log(CO2/CO2_0) | k | ChgVar |
|---|---|---|---|---|---|---|---|
| 2.344 | 17.6 | 2.090 | 380.7 | ||||
| 2.340 | 17.6 | 2.090 | 387.4 | 6.7 | 0.0174461 | -4.3615219 | TA |
| 2.344 | 18.6 | 2.090 | 396.8 | 16.1 | 0.0414207 | 0.0414207 | T |
| 2.344 | 17.6 | 2.096 | 392.7 | 12.0 | 0.0310343 | 5.1723830 | DIC |
| 34.8 | 0.0899011 | ALL | |||||
| 2.340 | 18.6 | 2.096 | 416.5 | 35.8 | 0.0898748 | ALL |
On peut dès lors considérer que
\[ log(CO_2/CO_2^0)\ =\ \alpha_{TA} \Delta_{TA}\ +\ \alpha_T \Delta _T\ +\ \alpha _{DIC} \Delta _{DIC} \tag{6.19}\]
Le calculateur en ligne fournit les valeurs de TA, T et DIC pour les scénarios Preindustrial et Modern, sans détailler le choix de leurs valeurs. Les références citées dans l’onglet chemistry du calculateur permettraient vraisemblablement d’en savoir plus, mais la matière est terriblement compliquée et nous ne pouvons que nous en remettre à l’expertise des auteurs du calculateur.
Dans un espace à 3 dimensions TA, T et DIC, nous disposons de 2 points correspondants à chaque scénario et supposons que l’évolution entre les 2 scénarios a suivi la droite entre ces 2 points, ce qui revient à considérer qu’il y a un couplage linéaire entre les 3 variables au cours de l’évolution entre les états Preindustrial et Modern.
Si s est un paramètre compris entre 0 et 1, et si les indices 0 et 1 correspondent respectivement aux états Preindustrial et Modern, l’équation paramétrique de cette droite prend la forme suivante :
\[ \begin{align} TA(s) & = s * (TA_1 – TA_0) + TA_0 \\ T(s) & = s * (T_1 – T_0) + T_0 \\ DIC(s) & = s * (DIC_1 – DIC_0) + TA_0 \end{align} \tag{6.20}\]
ou de manière équivalente :
\[ \begin{align} s & = (TA(s) – TA_0) / (TA_1 – TA_0) \\ & = (T(s) – T_0) / (T_1 – T_0) \\ & = (DIC(s) – DIC_0) / (DIC_1 – DIC_0) \end{align} \tag{6.21}\]
Si l’on fixe une des variables, on peut en déduire s et calculer ensuite les 2 autres variables. Ceci ne préjuge en rien d’un effet de causalité d’une variable par rapport aux 2 autres, la seule hypothèse qui est faite est celle d’un couplage linéaire entre les 3 variables.
En fixant la température, on peut dès lors considérer que \(\Delta_{TA}\) et \(\Delta_{DIC}\) sont proportionnels à \(\Delta_{T}\). On peut alors regrouper les termes de l’Équation 6.19 et on retrouve la relation classique:
\[ \log (\mathit{CO}_2/\mathit{CO}_2^0)\ =\ \alpha \Delta _T \tag{6.22}\]
En donnant à s quelques valeurs uniformément réparties dans l’intervalle [0,1], on peut calculer les valeurs de TA, T et DIC au moyen des formules précédentes et injecter ces valeurs dans le calculateur en ligne pour en déduire la pCO2.
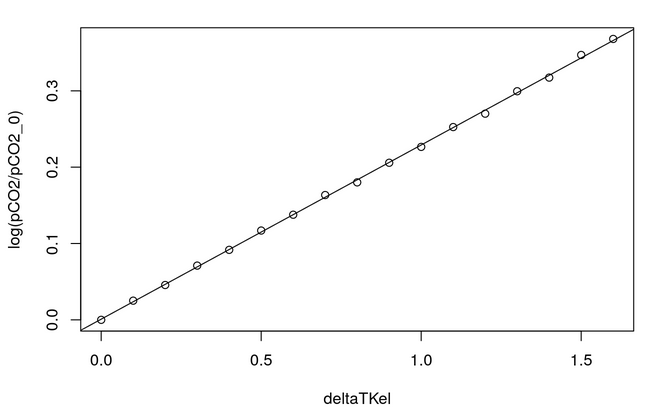
Il n’y a rien d’intuitif dans la chimie carbonatée de l’eau de mer, et il est assez surprenant de constater qu’en faisant les calculs décrits ci-dessus, on obtient une relation linéaire entre le log de la pCO2 et la température, comme dans la formule de Henry - van ’t Hoff. Voir Table 6.2, Figure 6.3 et Figure 6.4.
| Scenario | TA | T | DIC | pCO2 |
|---|---|---|---|---|
| Preindustrial | 2.311000 | 16.0 | 2.0020 | 263.5000 |
| 2.313063 | 16.1 | 2.0075 | 270.2000 | |
| 2.315125 | 16.2 | 2.0130 | 275.8000 | |
| 2.317188 | 16.3 | 2.0185 | 282.9000 | |
| 2.319250 | 16.4 | 2.0240 | 288.8000 | |
| 2.321312 | 16.5 | 2.0295 | 296.2000 | |
| 2.323375 | 16.6 | 2.0350 | 302.4000 | |
| 2.325438 | 16.7 | 2.0405 | 310.2500 | |
| 2.327500 | 16.8 | 2.0460 | 315.4500 | |
| 2.329563 | 16.9 | 2.0515 | 323.7000 | |
| 2.331625 | 17.0 | 2.0570 | 330.5000 | |
| 2.333687 | 17.1 | 2.0625 | 339.2000 | |
| 2.335750 | 17.2 | 2.0680 | 345.2333 | |
| 2.337813 | 17.3 | 2.0735 | 355.5000 | |
| 2.339875 | 17.4 | 2.0790 | 361.8667 | |
| 2.341937 | 17.5 | 2.0845 | 372.7500 | |
| Modern | 2.344000 | 17.6 | 2.0900 | 380.7000 |
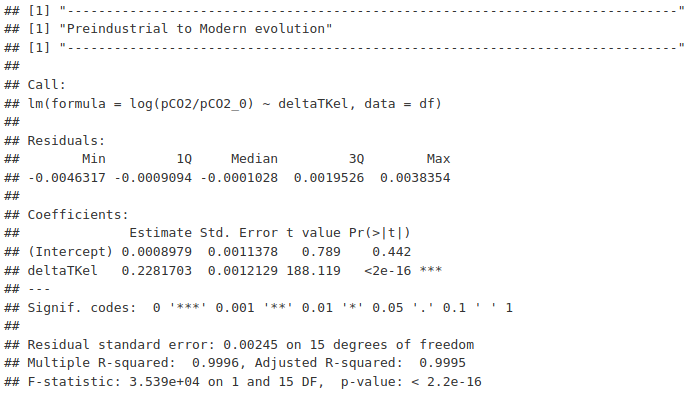
La relation trouvée est la suivante :
\[ \log (\mathit{CO}_2)\ =\ \log (263.5)\ +\ 0.2281703\ \Delta T \tag{6.23}\]
Ce qui est remarquable, c’est que le coefficient de \(\Delta T\) (0.22817) de l’Équation 6.23 est très proche de celui de la Figure 6.8 de l’analyse de la Section 6.7.1 (0.25718). Cette dernière analyse a été effectuée sur base de la température océanique hadsst3 et du CO2 naturel obtenu en déduisant du CO2 de Mauna Loa les émissions anthropiques en tenant compte de leur décroissance exponentielle avec une constante de temps de résidence de 15 ans. Cette dernière valeur a été observée lors de la décroissance du \(^{14}C\) après l’arrêt des essais thermonucléaires atmosphériques.
Ceci conforte à la fois la constante de 15 ans, l’équilibre de Henry – van ’t Hoff du calculateur en ligne de la pCO2 et celui déduit des observations de la température océanique et du CO2 naturel.
L’Équation 6.23 permet de calculer la variation de CO2 pour une variation de température donnée. L’équilibre étant bidirectionnel, la formule peut également être lue en sens inverse pour calculer la variation de température suite à une variation de CO2.
On peut ainsi évaluer l’augmentation de température due au cumul des émissions anthropiques depuis l’ère préindustrielle, lorsque l’équilibre des pCO2 océanique et atmosphérique sera atteint.
Voir Table 6.3.
| Total carbone anthropique (CDIAC) | 4.02068e+05 | millions de tonnes de carbone |
| 4.02068e+02 | Peta grammes de carbone | |
| Suivant la figure Cycle du carbone (AR5 WG1) | ||
| Atmosphere | 5.89000e+02 | Peta grammes de carbone |
| Surface ocean | 9.00000e+02 | Peta grammes de carbone |
| Intermediate & deep sea | 3.71000e+04 | Peta grammes de carbone |
| Augmentation relative de carbone | 1.04192e-02 | |
| Augmentation de température Suivant Henry – van ‘t Hoff Avec coeff de 0.228 | 4.54620e-02 | °C |
Les quantités de carbone proviennent du cycle du carbone d’après le GIEC AR5 WG1 Chapitre 6. Voir Figure 6.20.
L’impact du total cumulé du carbone anthropique sur la température est inférieur à 0.05 °C.
Suivant le même principe, on peut calculer l’augmentation de température pour un doublement de la pCO2. On obtient \(\Delta T=\log (2)/0.228\ =\ 3.04\ °C\). Cette valeur est importante, mais est complètement irréaliste, parce que pour doubler la pCO2 , il faut doubler la quantité de carbone atmosphérique ET la quantité de carbone océanique qui est environ 50 fois plus importante. Pour la même raison, la capture et le stockage du carbone est une ineptie. Si on retirait de l’atmosphère le total cumulé du carbone anthropique émis, on n’obtiendrait qu’une diminution de température de 0.045 °C.
6.3 Analyse CT.1 : CO2 et loi de Henry
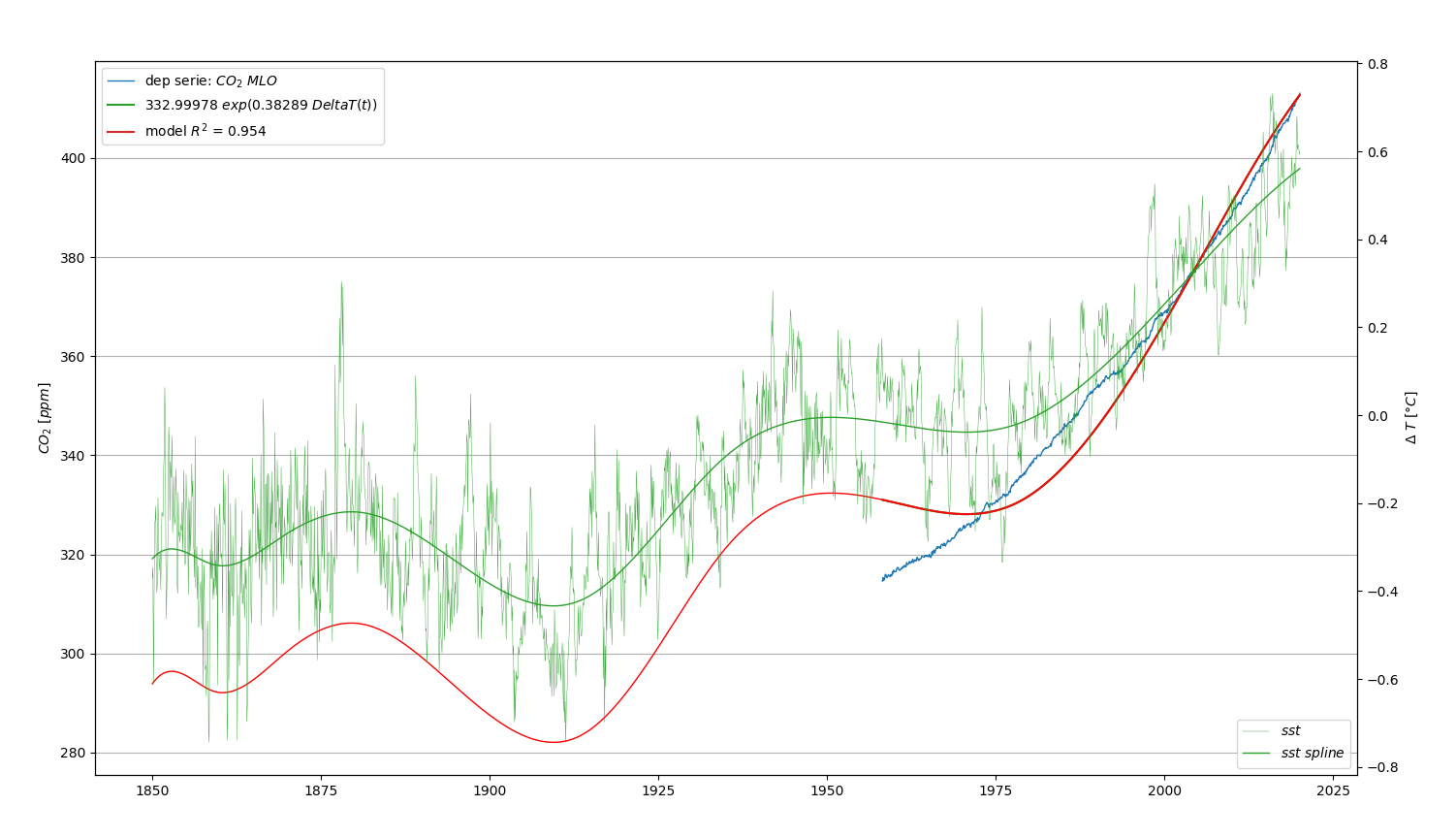
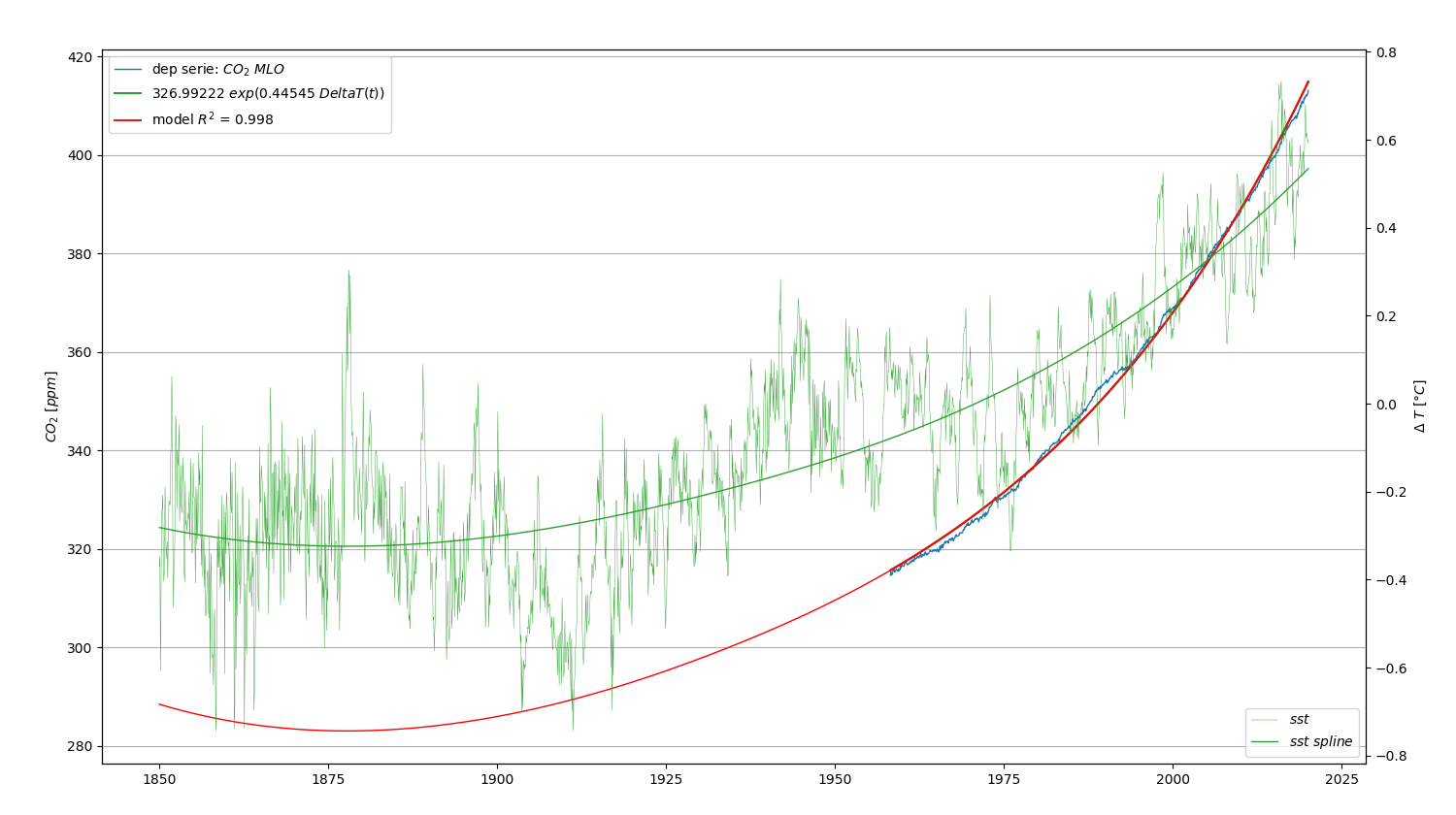
Régression du CO2Mauna Loa par la température hadsst3.
Voir Figure 6.5
| Parameter | Value | 95% interval |
|---|---|---|
| expDeltaT | 333.000000 | 0.17% |
| expDeltaT_a | 0.382886 | 1.55% |
6.4 Analyse CT.2 : CO2 et loi de Henry (bis)
Cette analyse est identique à l’analyse CT.1, mais avec un lissage par spline plus appuyé.
Voir Figure 6.6
| Parameter | Value | 95% interval |
|---|---|---|
| expDeltaT | 326.992000 | 0.04% |
| expDeltaT_a | 0.445451 | 0.32% |
6.5 Analyse CT.3 : Modèle “Constant airborne fraction” du GIEC
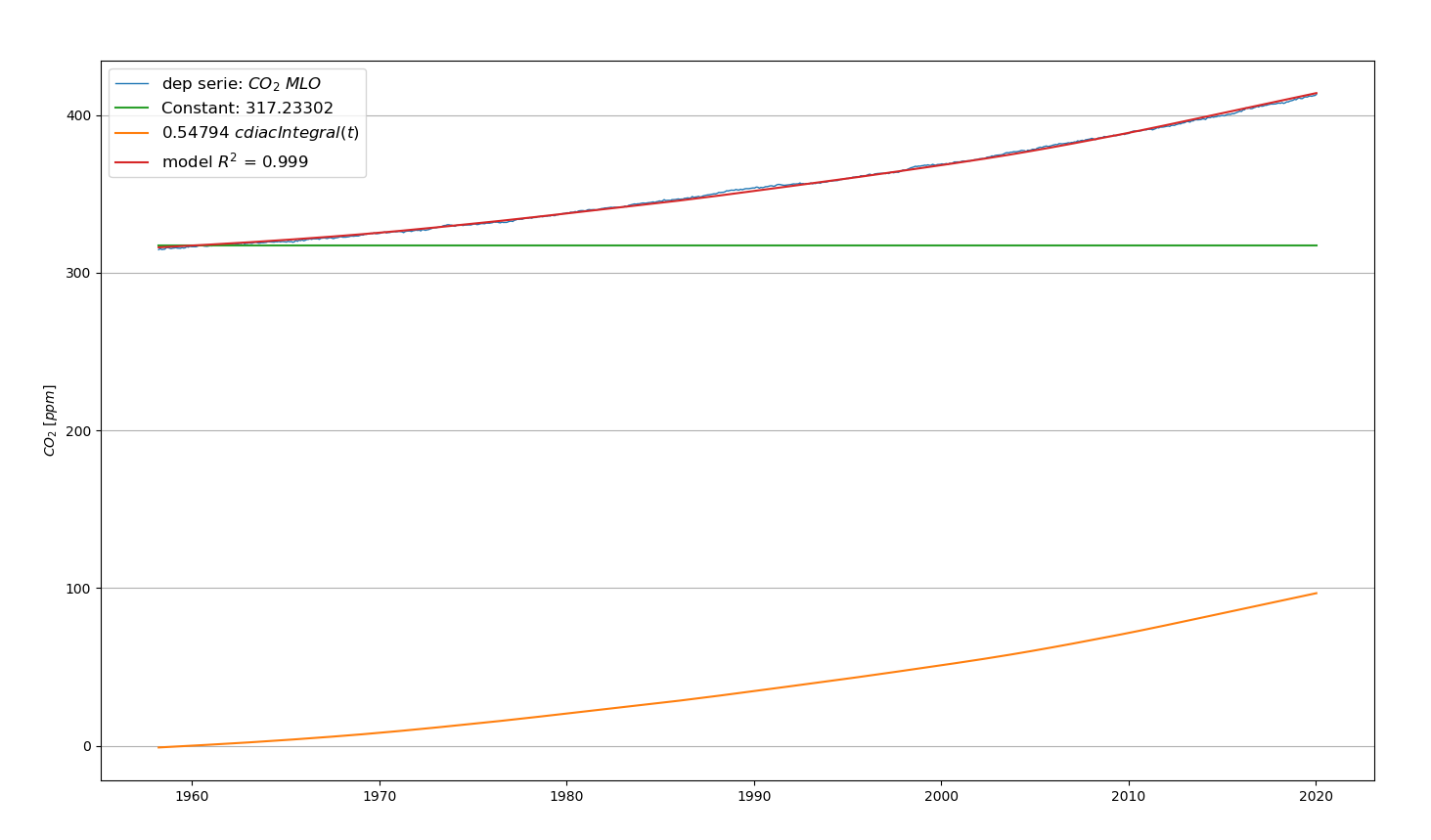
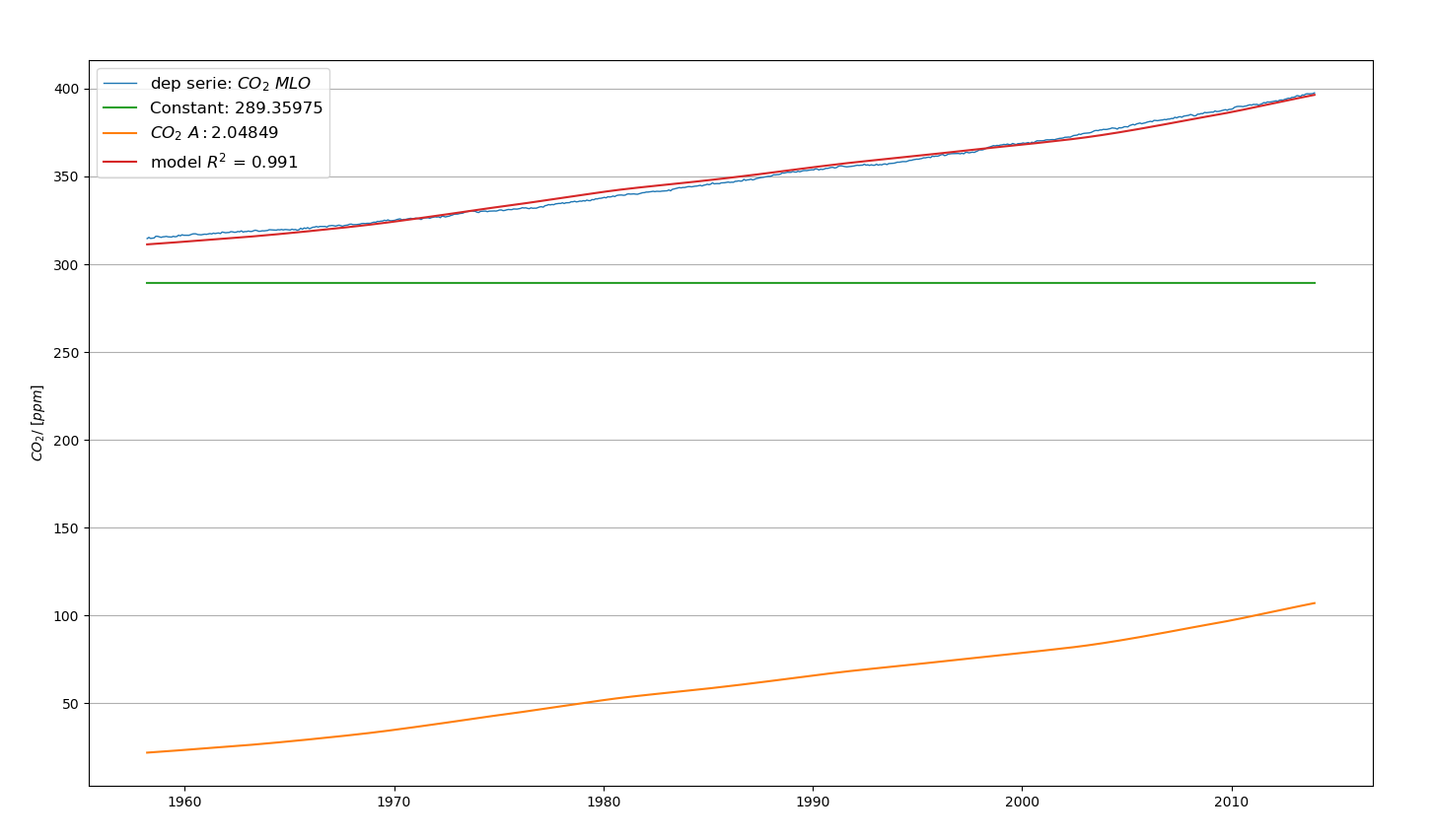
C’est une analyse de régression entre la concentration en CO2 (Mauna Loa sans variation saisonnière) et les émissions cumulées de CO2 anthropique depuis 1960.
Les émissions annuelles proviennent de (« CDIAC Global CO2 Emissions »). Un facteur de 2120 a été utilisé pour les convertir en ppm.
Cette analyse est équivalente au modèle “Constant airborne fraction” du GIEC qui suppose que la croissance du taux de CO2 provient exclusivement d’une fraction constante des émissions cumulées. Le solde est vraisemblablement réabsorbé par les océans (en recherchant à rétablir l’équilibre de Henry - van t’Hoff) et la photosynthèse (avec un décalage de plusieurs saisons).
Voir Figure 6.7.
| Parameter | Value | 95% interval |
|---|---|---|
| constant | 317.233000 | 0.04% |
| cdiacIntegral | 0.547941 | 0.24% |
6.6 Discussion des analyses CT.1 à CT.3
Deux modèles complètement antagonistes peuvent expliquer le relevé de Mauna Loa avec un coefficient de corrélation quasiment parfait.
Dans le premier (analyses CT.1-2), la variation de la concentration en CO2 atmosphérique est entièrement régie par les échanges de CO2 entre l’océan et l’atmosphère et dépendent des variations de température des océans, température qui elle-même dépend essentiellement de l’activité solaire et de ses variations. Les émissions anthropiques sont indiscernables des flux naturels. Le système n’est jamais à l’équilibre, mais tend par transfert de chaleur et matière entre l’océan et l’atmosphère, vers un équilibre donné pour les concentrations par les lois de Henry et van ’t Hoff, et pour les échanges de chaleur par l’égalité des températures de l’océan et de l’atmosphère. Toute variation de température océanique provoque des changements de la concentration atmosphérique en CO2. Toute augmentation de CO2 atmosphérique se traduit par une dissolution accrue de CO2 dans l’océan, ou son inverse, et une très légère modification de la température océanique. En supposant que la teneur en CO2 observée est égale à celle de l’équilibre de Henry – van ’t Hoff qui n’est quasiment pas affectée par les émissions anthropiques, ce modèle revient à considérer que le temps de résidence de ces dernières est nul.
Dans le second (analyse CT.3), la variation du taux de CO2 est entièrement d’origine anthropique avec un temps de résidence infini, et il n’y a pas d’émission nette naturelle.
Toute combinaison linéaire de ces modèles fournira un autre modèle aussi parfait du point de vue de son ajustement aux données expérimentales de Mauna Loa. Les analyses de régression ne permettent pas de définir la meilleure combinaison.
L’analyse CT.3 suggère que l’augmentation anthropique du CO2 est égale à une fraction de l’augmentation totale du CO2. L’augmentation naturelle du CO2 s’obtient alors par différence, ce qui évite de devoir la modéliser avec les nombreuses inconnues qui y sont liées. Cette approche est schématisée à la Figure 6.8.
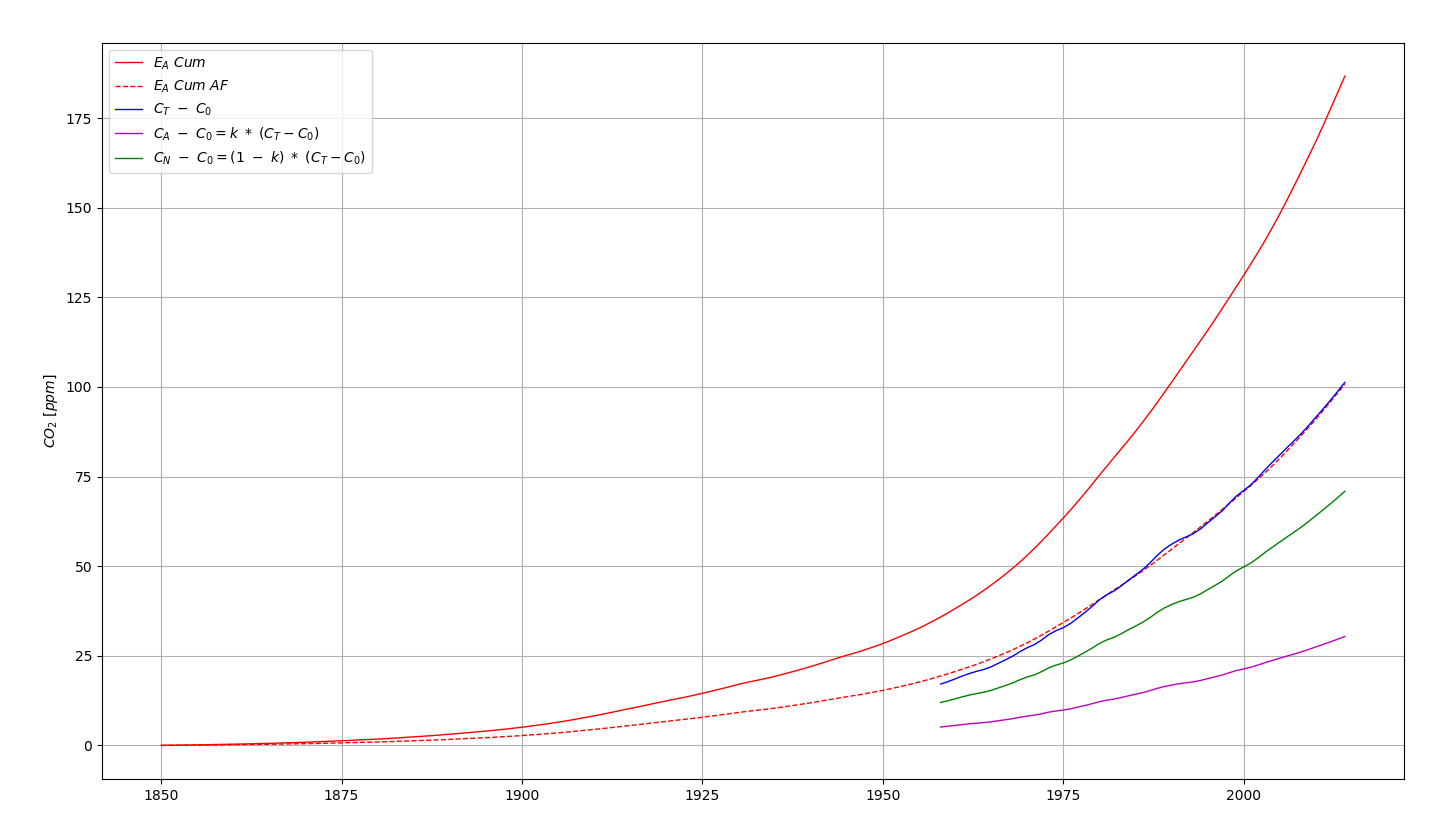
La fraction k correspondant à l’augmentation de la concentration en CO2 anthropique ne peut cependant être choisie arbitrairement. Il y a des contraintes à respecter qui seront évaluées dans l’analyse suivante (CT.4).
6.7 Le CO2 naturel et la loi de Henry – van’t Hoff
6.7.1 Analyse CT.4 : décroissance exponentielle du CO2 anthropique
L’arrêt des essais atmosphériques de bombes thermonucléaires au début des années 1960 montre une décroissance exponentielle du \(^{14}C\) libéré par les explosions, avec une constante de temps d’environ 15 ans (Harde 2019).
Si on fait l’hypothèse que le CO2 d’origine anthropique se comporte de la même manière, sa concentration peut être décrite par l’équation suivante, dans laquelle \(C_A\) représente la concentration en CO2 anthropique, \(e_A\) les émissions anthropiques, et \(\tau\) une constante de temps de résidence :
\[ \frac{\mathit{dC}_A}{\mathit{dt}}\ =\ e_A\ -\ \frac{C_A}{\tau } \tag{6.24}\]
Cette équation peut être intégrée numériquement. La concentration en CO2 naturel (\(C_N\)) s’obtient alors simplement par différence avec le taux observé (\(C_{obs}\)):
\[ C_N\ =\ C_{\mathit{obs}}\ -\ C_A \tag{6.25}\]
On peut ensuite faire une analyse de régression analogue à l’analyse CT.1 ou CT.2 pour la concentration en CO2 naturel.
La constante de 15 ans est une valeur apparente. La valeur réelle pourrait être plus faible à cause de phénomènes de réémission (moins d’une décennie selon (Harde 2019).
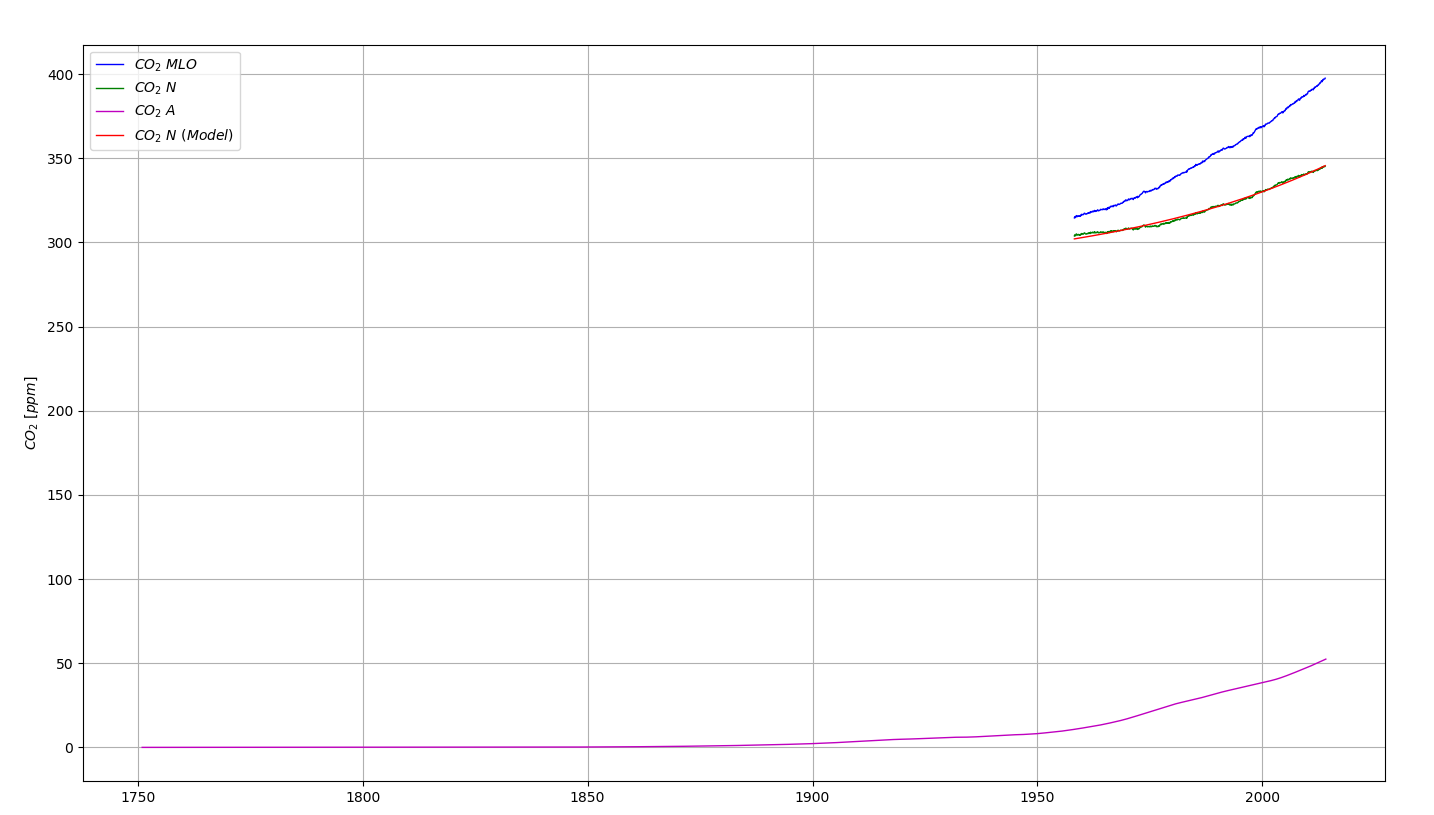
La formule qui lie le CO2 naturel à l’anomalie de température peut s’écrire sous forme logarithmique :
\[ \log (\mathit{CO}_{2N})\ =\ \log (308.32254)\ +\ 0.2518\ \Delta T \tag{6.26}\]
L’analyse de régression entre le CO2 observé et le CO2 anthropique présente un très bon coefficient de corrélation. On retrouve l’aspect “airborne fraction” comme dans l’analyse CT.3, avec la différence importante que cette fraction n’est pas constante, mais dépend de la constante de temps de résidence. Voir Figure 6.11
En faisant varier la constante de temps de résidence \(\tau\) on peut construire un tableau pour vérifier les contraintes liées aux teneurs en CO2 anthropique et naturel. Ces contraintes ont été analysées par J.C. Maurin dans deux articles en plusieurs parties : (Maurin 2018a), (Maurin 2018b), (Maurin 2018c), (Maurin 2018d) et (Maurin 2019a), (Maurin 2019b), (Maurin 2019c).
Ces études sont basées sur les abondances isotopiques du carbone.
Une première contrainte porte sur le \(\Delta^{14}C\) lié à l’effet Suess qui doit être compris entre -15‰ et -25‰ en 1950. Cette contrainte limite la valeur du CO2 anthropique de cette époque à une valeur comprise entre 4.7 et 7.8 ppm.
Une deuxième contrainte porte sur le \(\delta^{13}C\) qui dépend de l’usage de combustibles fossiles. Le \(\delta^{13}C\) valait -7.6‰ en 1980 et -8.3‰ en 2010.
Quelques éclaircissements concernant le \(\delta^{13}C\)
Les mesures climatiques directes n’ont que deux à trois siècle d’existence. Pour des valeurs plus anciennes il faut recourir à des « proxies ». C’est ainsi que l’analyse des bulles de gaz inclues dans des carottes glaciaires s’est avérée capable de fournir des estimations climatiques sur une période atteignant 800 000 ans (Jouzel, 1987, https://www.nature.com/articles/329403a0).
Le carbone est un des éléments les plus abondants sur Terre. Pour près de 99% il est constitué de l’isotope \(^{12}C\). L’isotope \(^{13}C\) représente environ 1.1%, et l’istope \(^{14}C\) est présent à l’état de traces. Il s’agit d’un isotope instable (période de demi-vie de 5 700 ans)
Le CO2 formé par ces isotopes \(^{13}C\) et \(^{14}C\) étant beaucoup moins abondant que celui formé à partir de \(^{12}C\), les plantes, utilisant le CO2 pour leur photosynthèse, sont appauvries en ces isotopes « rares » et, dans les combustibles fossiles, formés il y a très longtemps, et quasiment totalement à partir de végétaux, cette « signature » est encore amplifiée davantage. Ces combustibles fossiles sont considérablement appauvris en \(^{13}C\), tandis que le \(^{14}C\) a quasiment totalement disparu.
Un paramètre a été défini pour distinguer le CO2 d’origine organique de celui d’origine minérale, à partir d’un échantillon de référence (prélevé à une date connue) :
\[\delta^{13}C=\frac{[\frac{^{13}C}{^{12}C}]_{echantillon}-[\frac{^{13}C}{^{12}C}]_{reference}} {[\frac{^{13}C}{^{12}C}]_{reference}} \cdot 1000\]
\(\delta^{13}C\), qui s’exprime en pour mille, est toujours négatif pour le carbone d’origine organique ( de l’ordre de -26‰ pour les combustibles fossiles) et toujours positif pour celui d’origine minérale (de l’ordre de 4‰ ). A partir de là, en mesurant l’augmentation de CO2 atmosphérique et les changements du \(\delta^{13}C\) dans l’atmosphère, il est possible, aux erreurs de calibrage près (*), de retrouver le taux de CO2 anthropique (résultant de l’utilisation des combustibles fossiles) contribuant à l’augmentation de la concentration en CO2 atmosphérique. Le calcul est quelque peu biaisé par la contribution des feux de forêt, présentant un \(\delta^{13}C\), certes moindre que celui des combustibles fossiles, l’âge des arbres étant moindre que celui desdits combustibles fossiles, mais significatif et toujours négatif. (*)
Depuis 1990, le \(\delta^{13}C\) atmosphérique est passé de -6.2 à -8.5‰. Ce qui a été interprété par le GIEC comme une preuve d’accumulation de carbone d’origine anthropique dans l’atmosphère. Mais cela ne prouve nullement que l’entièreté de l’augmentation en CO2 atmosphérique soit exclusivement d’origine anthropique. (*)
(inspiré de Philippe Charlez, l’utopie de la croissance verte, Lafont 2021, pg 350 et suivantes) [ISBN 978-2-492545-03-0].(*) texte de l’auteur en italique
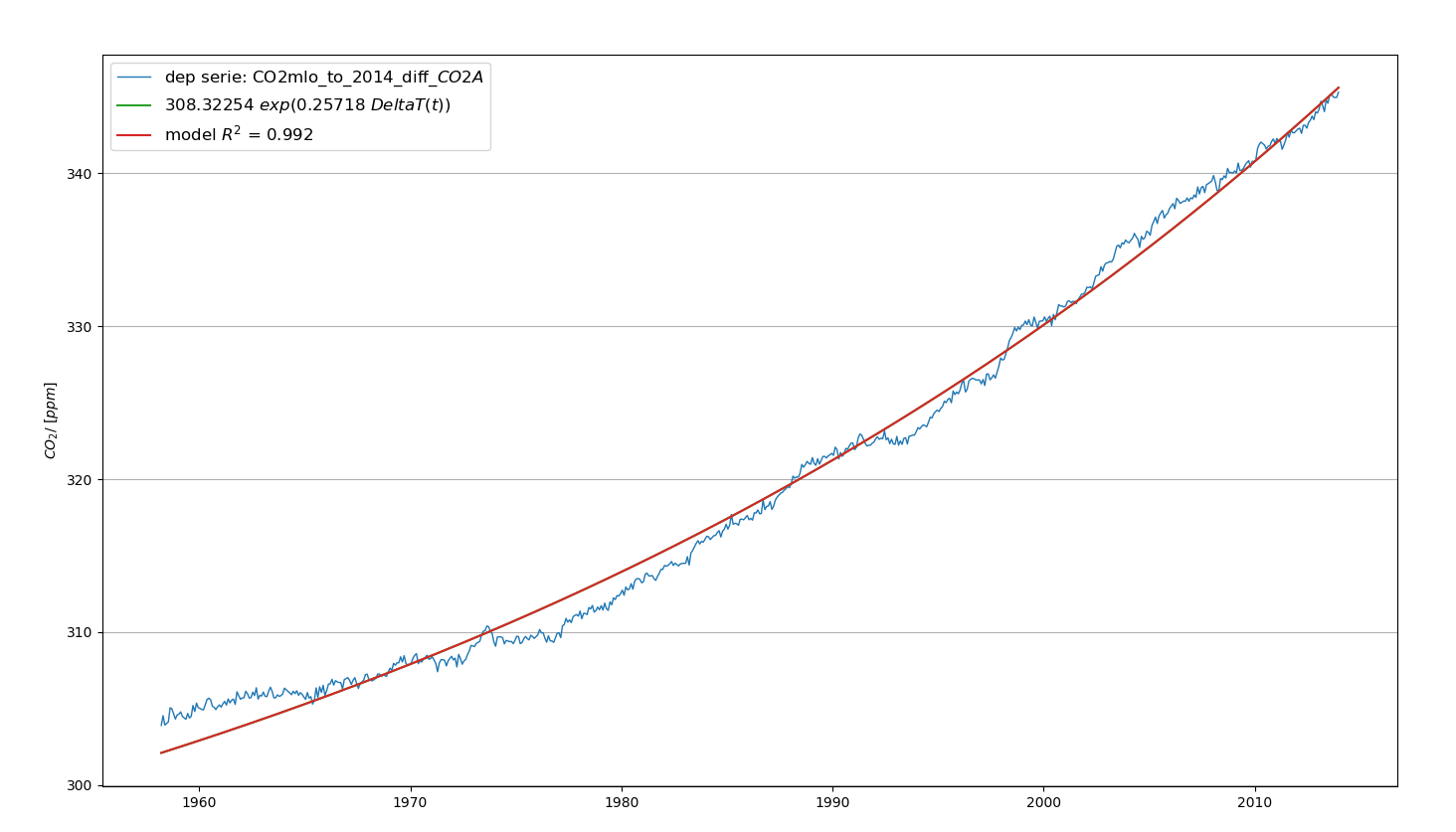
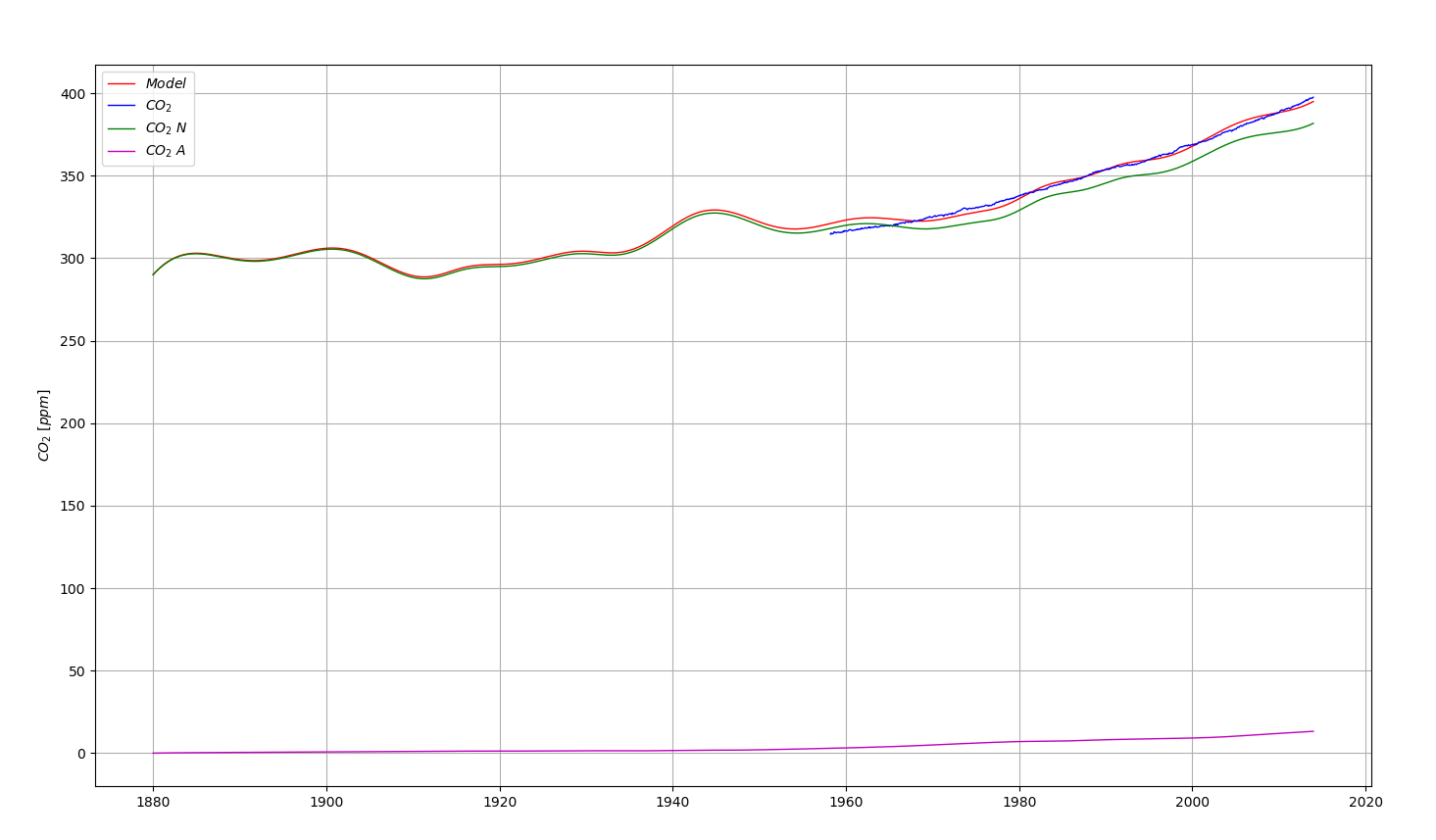
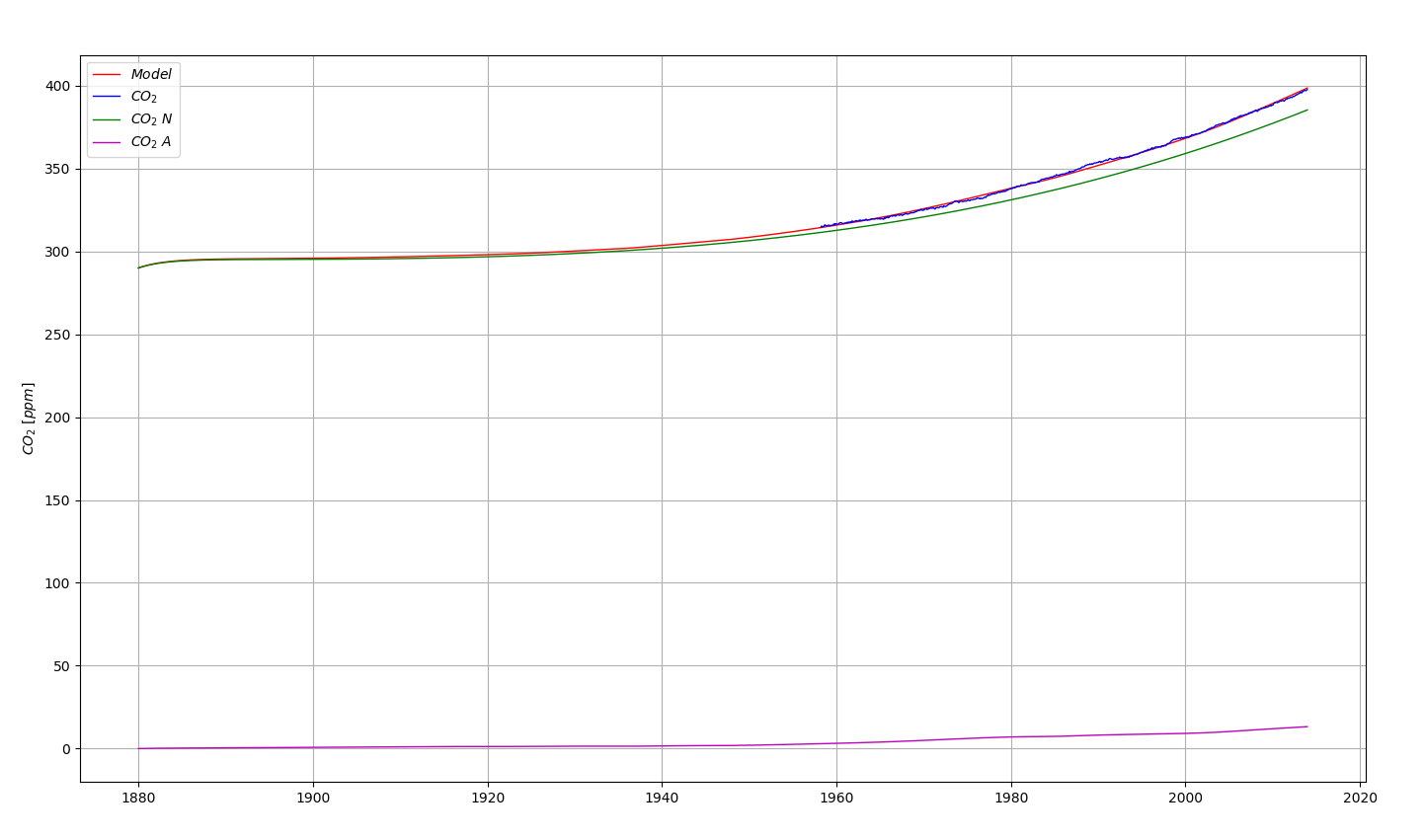
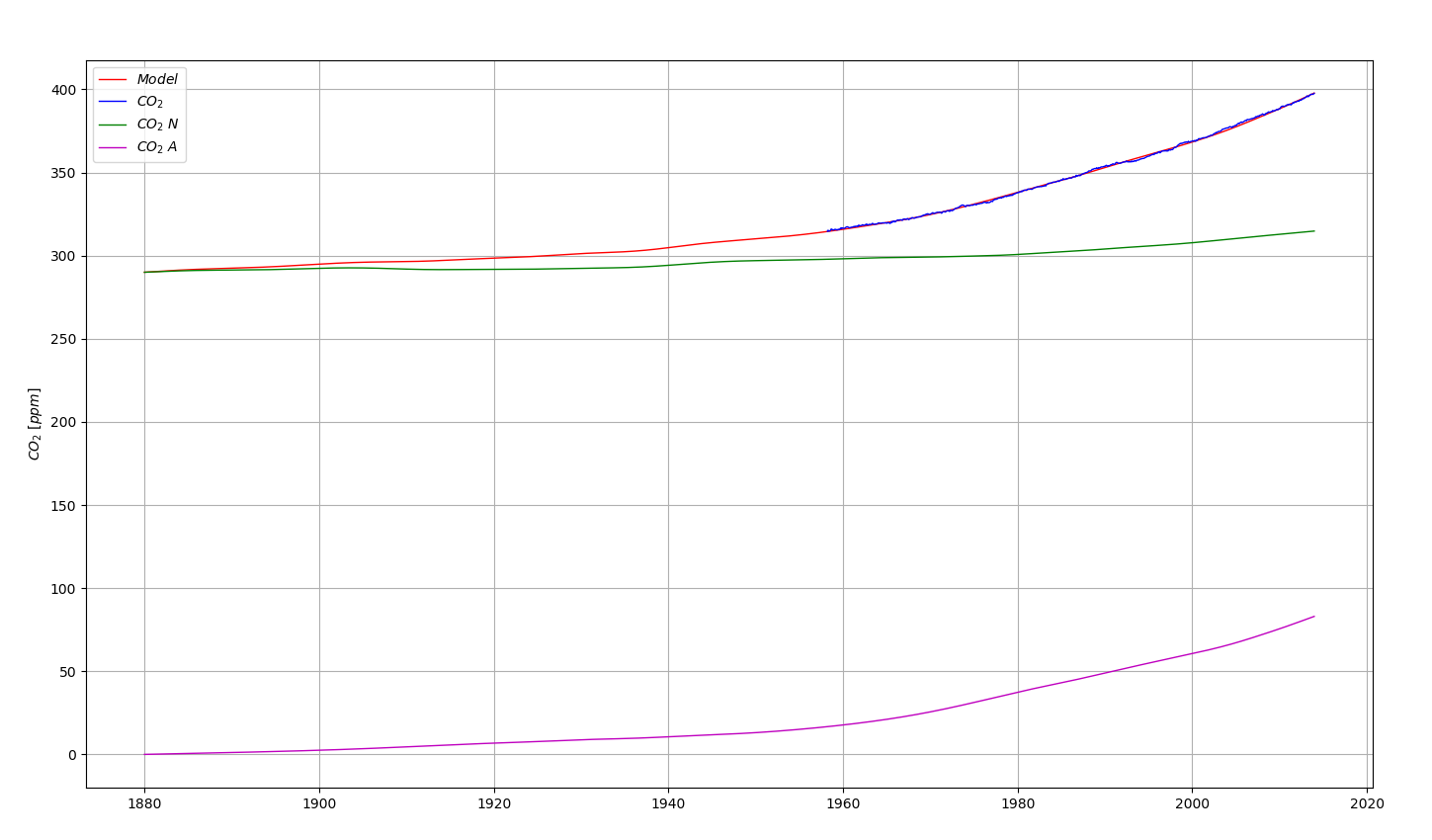
Ces contraintes ont été évaluées pour quelques valeurs de \(\tau\). Les analyses correspondantes, non reproduites ici, ont résumées dans la table Table 6.7).
| τ | Δ14C | CO2A | CO2 | CO2A | CO2N | CO2 | CO2A | CO2N | AF | k | δ13C |
| 7.7 | 15‰ | 4.7 | 337.9 | 15.8 | 322.1 | 388.3 | 27.7 | 360.6 | 15% | 0.27 | -7.55 |
| 10.6 | 20‰ | 6.2 | 337.9 | 20 | 317.9 | 388.3 | 36.2 | 352.1 | 20% | 0.37 | -7.87 |
| 14.1 | 25‰ | 7.8 | 337.9 | 24.3 | 313.6 | 388.3 | 45.3 | 343 | 25% | 0.46 | -8.22 |
L’évolution du CO2 anthropique (CO2A) est calculée sur base des émissions du CDIAC en tenant compte d’une décroissance exponentielle déterminée par une constante de temps \(\tau\). Par différence avec le CO2 relevé à Mauna Loa (CO2), on obtient le CO2 naturel (CO2N). La valeur de \(\tau\) a été ajustée pour que le CO2A prenne les valeurs de 4.7, 6.2 et 7.8 ppm en 1950, qui correspondent à des valeurs de \(\Delta^{14}C\) de 15, 20 et 25‰. Les analyses analogues à celles de la Figure 6.11 déterminent le coefficient k, égal à l’inverse du coefficient du CO2A associé à la courbe orange de cette figure. La colonne AF est égale à ce coefficient k multiplié par 0.548 qui correspond au paramètre cdiacIntegral de la Figure 6.7. Elle correspond à l’ “airborne fraction” qui devrait être utilisée à la place de la valeur du GIEC. Finalement le \(\delta^{13}C\) en 2010 est calculé par la formule
\[ \delta^{13}C=\frac{-[\mathit{CO}_2^{1980}\ast 7.6+(\mathit{CO}_{2A}^{2010}-\mathit{CO}_{2A}^{1980})\ast 29+(\mathit{CO}_{2N}^{2010}-\mathit{CO}_{2N}^{1980})\ast 0.5]}{\mathit{CO}_2^{2010}} \tag{6.27}\]
Il n’y a que la valeur de \(\tau\) d’environ 14 ans qui respecte (à peu près) toutes les contraintes. Elle correspond bien aux observations après la fin des essais thermonucléaires atmosphériques.
Dans quelle mesure ces contraintes sont-elles absolues ? (Harde 2019) a présenté un modèle légèrement différent avec une valeur de \(\tau\) de 3 ans, en mentionnant plusieurs arguments pour lesquels ces contraintes ne doivent pas être prises à la lettre. Ce modèle fait l’objet de l’analyse suivante.
6.7.2 Analyse CT.5 : le modèle de Harde
Dans sa modélisation du cycle du CO2, le GIEC considère que les émissions naturelles de CO2 sont rapidement absorbées et que les émissions anthropiques demeurent très longtemps dans l’atmosphère. Cette hypothèse est en contradiction avec le Principe d’indiscernabilité ; quelle que soit l’abondance isotopique dans un flux de CO2 donné, les molécules se comportent de la même façon, macroscopiquement, d’un point de vue thermodynamique et physico-chimique. C’est par ailleurs la propriété caractéristique qui justifie l’utilisation de marqueurs radioactifs dans un large spectre d’utilisations..
Dans son modèle, Harde considère beaucoup plus logiquement que les émissions naturelles et anthropiques réagissent de la même façon. Les molécules de CO2 d’origine naturelle ou anthropique sont en effet indiscernables. Elles se comportent de la même façon d’un point de vue de la thermodynamique et de la physico-chimie macroscopique.
L’évolution du CO2 atmosphérique est régie par l’équation suivante, toujours identique à celle d’un mélangeur parfait, mais avec deux flux entrants:
\[ \frac{\mathit{dC}}{\mathit{dt}}\ =\ e_N\ +\ e_A\ -\ \frac C{\tau } \tag{6.28}\]
| \(C\) | représente la concentration en CO2 atmosphérique, |
| \(e_N\) | les émissions naturelles, |
| \(e_A\) | les émissions anthropiques, |
| \(\tau\) | le temps de résidence (considéré comme un paramètre à ajuster). |
Les émissions naturelles sont supposées varier linéairement avec l’anomalie de température ΔT:
\[ e_N\ =\ a\ +\ b\Delta T \tag{6.29}\]
Dans cette équation, a et b représentent des constantes.
Le paramètre \(\tau\) sera considéré comme constant dans cette analyse.
L’Équation 6.28 et l’Équation 6.29 peuvent être remaniées comme suit:
\[ \frac{\mathit{dC}}{\mathit{dt}}\ -\ e_A\ +\ \frac C{\tau }\ =\ \ a\ +\ b\Delta T \tag{6.30}\]
Le calcul est fait en deux étapes.
Les paramètres a et b sont d’abord calculés par une analyse de régression avec le terme de gauche de l’Équation 6.30 comme variable dépendante.
Ensuite, l’Équation 6.28 est intégrée numériquement pour reconstruire l’évolution du taux de CO2 dans le temps.
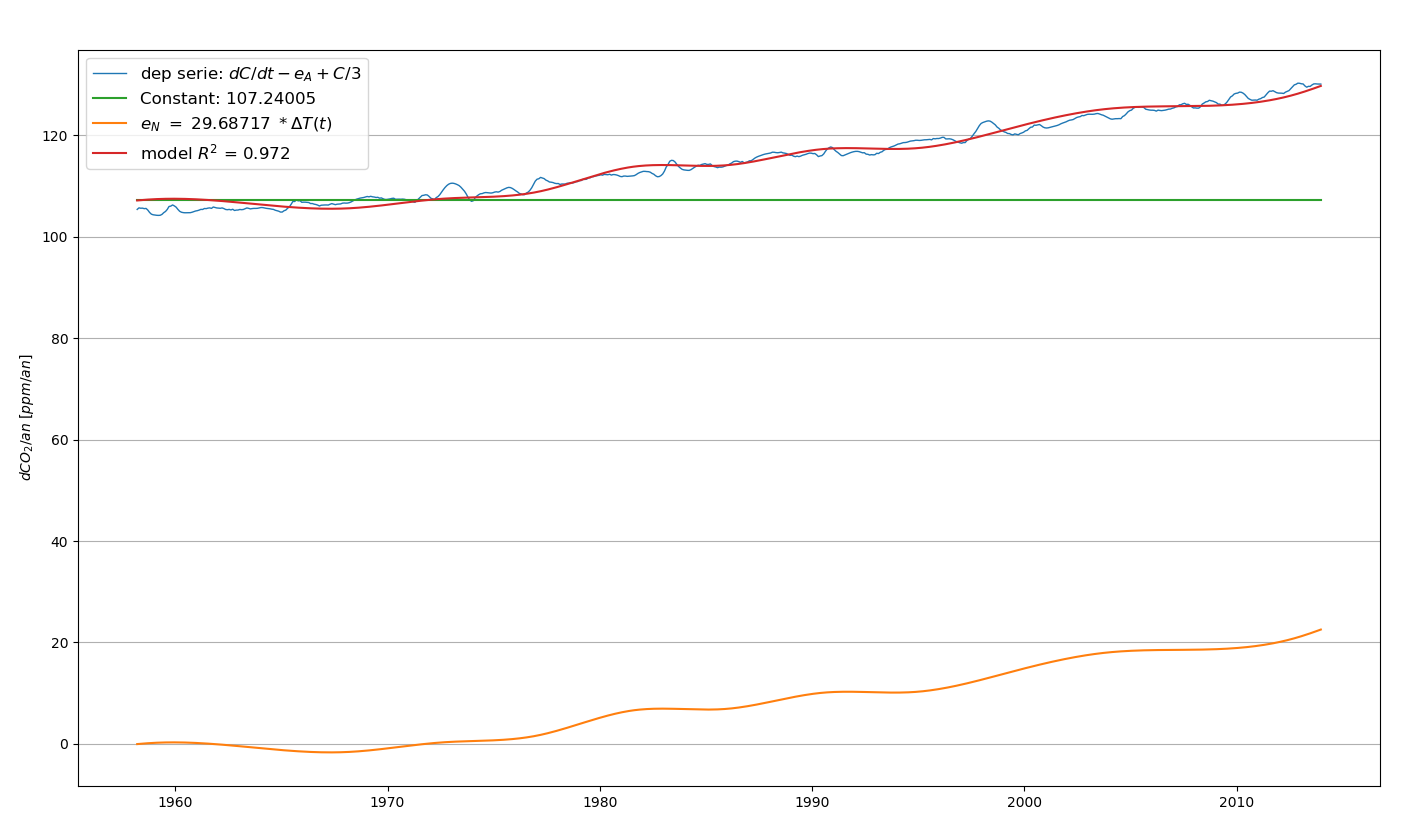
En utilisant comme Harde la série de température (« GISS data ») et une valeur de 3 ans pour \(\tau\), on obtient les résultats suivants. Voir Figure 6.12, Figure 6.13 et Figure 6.14.
| Parameter | Value | 95% interval |
|---|---|---|
| constant | 107.2400 | 0.13% |
| ΔT | 29.6872 | 1.28% |
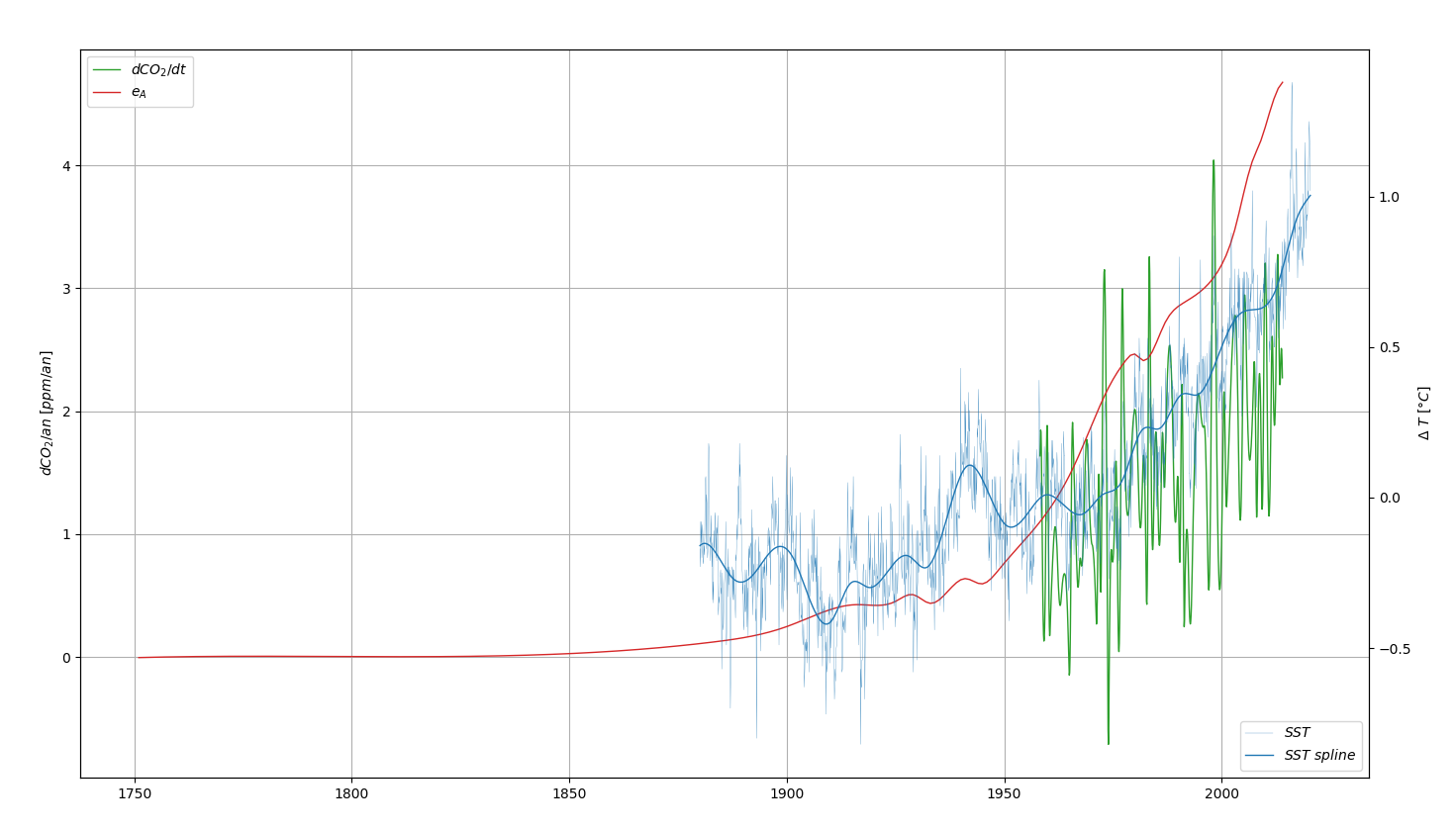
On retrouve quasiment le résultat de Harde:
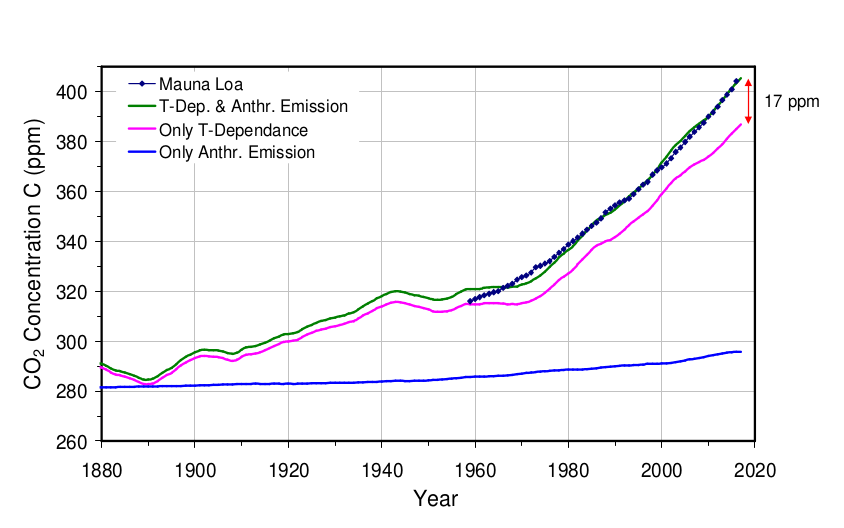
Dans les 2 cas, on peut noter que l’ajustement est moins bon entre 1960 et 1980.
Ce défaut peut être corrigé en conservant \(\tau\) égal à 3 ans et en lissant plus fortement l’anomalie de température. Voir Figure 6.16. On pourrait même prendre \(\tau\) égal à 1 an avec un ajustement tout aussi bon.
On obtient également un meilleur résultat en conservant le lissage initial et en utilisant une valeur de \(\tau\) égale à 30 ans. Voir Figure 6.17.
Les contraintes d’abondances isotopiques ont également été évaluées pour le modèle de Harde pour quelques valeurs de \(\tau\) en utilisant le même lissage qu’à la Figure 6.12. Elles sont reprises dans la table Table 6.9.
| τ | CO2A | CO2 | CO2A | CO2N | CO2 | CO2A | CO2N | δ13C |
| 3 | 2 | 337.9 | 7 | 330.9 | 388.3 | 12 | 376.3 | -7.05 |
| 14 | 7.8 | 337.9 | 24.2 | 313.7 | 388.3 | 45.1 | 343.2 | -8.21 |
| 30 | 13.1 | 337.9 | 37.4 | 300.5 | 388.3 | 75.6 | 312.7 | -9.48 |
Les colonnes ont la même signification que celles de la table Table 6.7. Ici aussi, une valeur de égale à 14 ans satisfait quasiment aux contraintes.
En vue de comparer le modèle de Harde avec le modèle simplifié de la Section 6.7.1, un calcul a été fait avec une valeur de \(\tau\) égale à 15 ans, identique à celle utilisée dans les analyses de la Figure 6.9 et de la Figure 6.10.
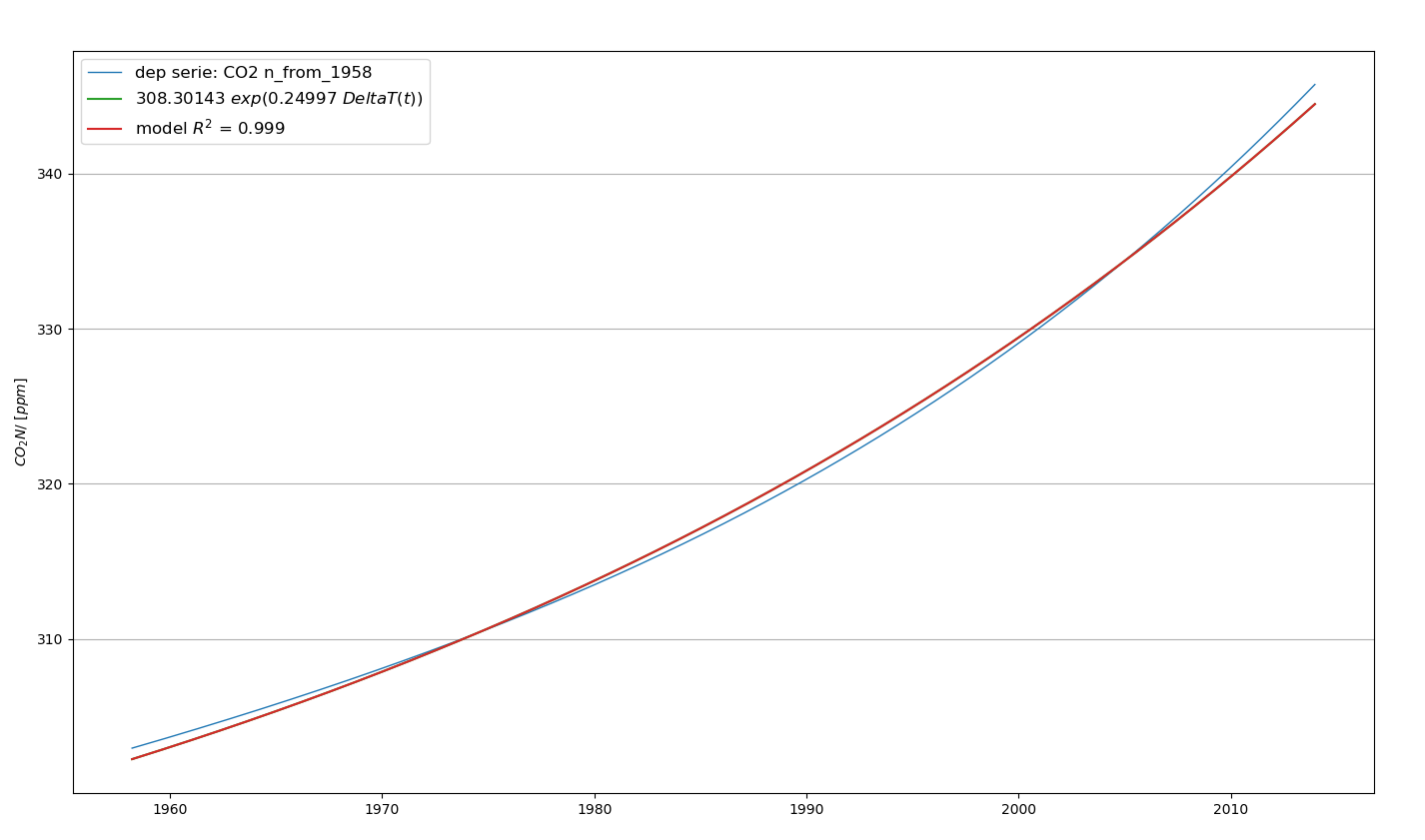
Une analyse de régression a été menée pour trouver la liaison entre le CO2 naturel et l’anomalie de température. Voir Figure 6.18.
La formule qui lie le CO2 naturel à l’anomalie de température peut s’écrire sous forme logarithmique :
\[ \log (\mathit{CO}_2N)\ =\ \log (308.30143)\ +\ 0.24997\ \Delta T \tag{6.31}\]
Cette équation est très proche de l’Équation 6.23 et quasiment identique à l’Équation 6.26.
On trouve des résultats analogues en utilisant la série de température hadsst3 au lieu de la série GISS.
6.7.3 Comparaison des formules de Henry – van ’t Hoff
Nous disposons de trois formules (Équation 6.23, Équation 6.26, Équation 6.31) qui décrivent l’équilibre entre le CO2 naturel et la température. Elles ont été obtenues par trois approches différentes.
La première (Équation 6.23) a été dérivée de l’étude d’un calculateur en ligne qui permet de résoudre les équations de la chimie carbonatée de l’eau de mer.
Les deux autres (Équation 6.26 et Équation 6.31) sont basées sur une estimation du CO2 naturel au départ des relevés du CO2 total, d’une anomalie de température et d’une constante de temps de résidence de 15 ans. Voir Figure 6.19.
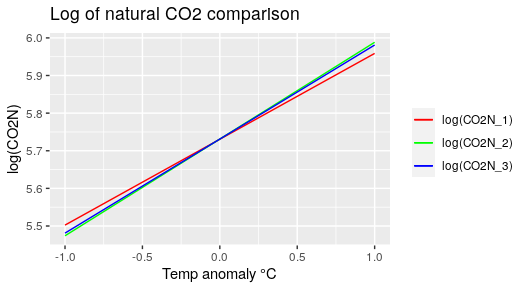
6.8 Considérations sur le cycle du carbone du GIEC
Une méthode alternative d’estimation du taux de CO2 anthropique (ou total) restant dans l’atmosphère, et de son temps de séjour, consiste à se baser sur les flux de carbone entre les divers réservoirs du cycle de carbone et sur les quantités de carbone qui s’y trouvent.
La Figure 6.20 reprend la synthèse de ces informations, telles qu’estimées par le GIEC, non pas sous forme de CO2 mais de carbone. Le rapport massique CO2/C = 44/12 (le rapport des masses molaires). Ces chiffres sont évidemment approximatifs (qui peut estimer exactement la quantité de carbone émise par chacun des pays existants ?), mais les marges d’erreur ne sont pas justifiées par le GIEC. Régulièrement de nouveaux flux de carbone sont identifiés, et les chiffres existants sont considérablement modifiés. Mais utilisons ces chiffres pour effectuer une petite démonstration par l’absurde de l’incohérence des hypothèses posées par le GIEC.
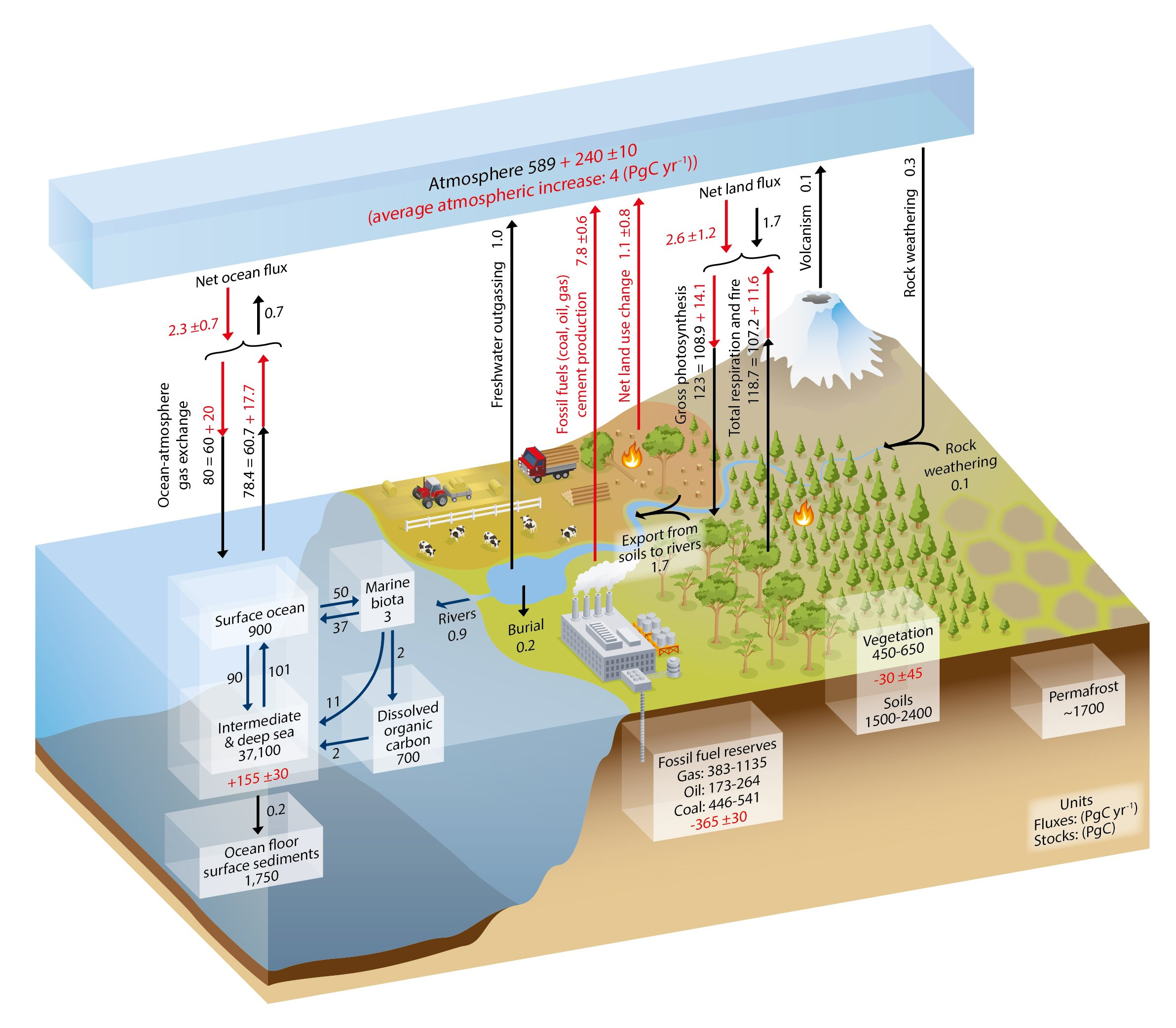
On constate, à partir de cette figure, que
La quantité totale de carbone dans l’atmosphère est estimée à 589 Pg
Le flux total entrant de carbone est égal à 207.1 Pg/an (78.4+1.0+7.8+1.1+118.7+0.1)
Le flux anthropique entrant (utilisation de combustibles fossiles et changement d’affectation des terres) est égal à 8.9 Pg/an (7.8+1.1)
Le flux total sortant de l’atmosphère est égal à 203.3 Pg/an (80+123+0.3)
Dès lors :
- La quantité de carbone ajoutée annuellement à l’atmosphère est la différence entre le flux entrant total et et le flux sortant total, soit 3.8 Pg/an
On en déduit que
Le temps de séjour moyen est par définition la masse de carbone dans l’atmosphère, divisée par le flux sortant total, soit 589 /203.3 = 2.90 années (une figure comparable à celles discutées précédemment dans ce texte)
Le temps nécessaire pour doubler la quantité de carbone dans l’atmosphère est de 589/3.8= 155 années, au rythme actuel d’émissions de CO2 (naturel et anthropique).
Le rapport de la quantité de carbone d’origine anthropique sur le flux entrant total est de 8.9/207.1 = 4.3 %
Le rapport entre l’augmentation annuelle de carbone piégé dans l’atmosphère et le flux anthropique est de 3.8 / 8.9 = 43 % (un chiffre à comparer à ceux des modèles développés dans les sections précédentes)
Rappelons cependant ici, qu’en vertu du Principe d’Indiscernabilité, le carbone d’origine anthropique ou naturelle a exactement les mêmes propriétés thermodynamiques et physico-chimiques macroscopiques, et cela quelle que soit l’abondance de l’un ou l’autre isotope de carbone dans l’un ou l’autre flux (cette abondance étant utilisée par le GIEC comme signature permettant d’identifier la contribution anthropique). Prétendre, comme le fait le GIEC, que l’accumulation de carbone dans l’atmosphère est uniquement d’origine anthropique, le monde naturel étant en équilibre statique permanent, relève de l’idéologie plus que de la science, pour ne pas dire du bon sens.
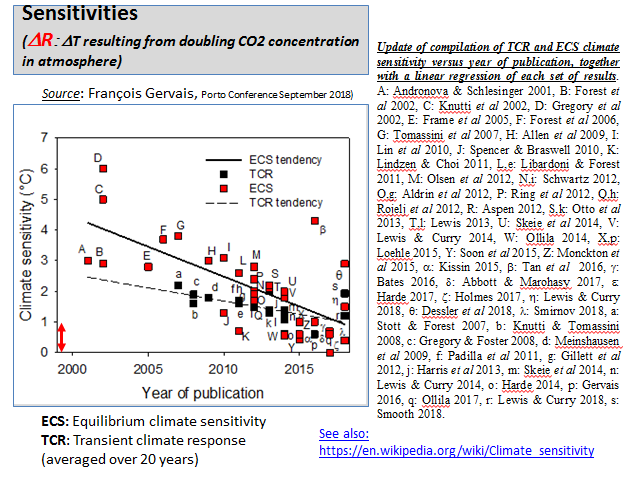
Remarquons également au passage que le temps nécessaire pour doubler la quantité de carbone dans l’atmosphère (et on vient de constater qu’il est de l’ordre d’un siècle et demi) est à la base du concept de sensibilité climatique : l’augmentation de température moyenne globale résultant d’un doublement de la quantité de CO2 (ou de carbone) dans l’atmosphère. Selon la théorie de l’effet de serre atmosphérique, doubler la quantité de carbone dans l’atmosphère provoquerait une augmentation de température de l’ordre de 1 à 10 degrés. Bien que les estimations les plus récentes penchent plutôt vers la limite inférieure de 1°C , voire en-dessous, (Voir Figure 6.21), le GIEC retient la valeur de 3.5°C, et les alarmistes prônent l’urgence de ramener cette augmentation de température à 1.5°C, sous peine, disent-ils d’atteindre un point de non-retour du dérèglement climatique (tipping point). Aucun fait scientifique ou expérimental ne permet de justifier cette crainte.
Mais, toujours dans la perspective d’une démonstration par l’absurde, on peut se demander quel serait l’effet d’une politique zéro carbone, décidée et implantée instantanément avec une efficacité totale (un objectif oh combien utopique) par un pays comme la Belgique ou la France. Effet, non pas sur les flux de carbone (un indicateur de moyens mis en œuvre), mais sur la température moyenne globale (l’indicateur d’objectif à atteindre):
Sensibilité climatique: 1 à 10°C
Flux total entrant dans l’atmosphère: 207.1 Pg /an
Flux d’origine anthropique: 8.9 Pg/an
Rapport du flux anthropique sur le flux total : 4.3 %
Fraction de flux anthropique émis par la France 1% (source OCDE)
Fraction de flux anthropique émis par la Belgique: 0.37 % (source OCDE)
Et donc, dans environ un siècle et demi (temps requis pour doubler la quantité de carbone présent dans l’atmosphère au rythme actuel des flux d’émission de carbone d’origine naturelle et anthropique), une politique zéro carbone réduira la température moyenne globale, si implantée
En France, de (1 à 10°C) * 0.043 * 0.01 ~ 0.0004 à 0.004 °C (entre quatre millièmes et quatre dix millièmes de degré C)
En Belgique, de (1 à 10°C) * 0.043 * 0.0037 ~ 1.6 10-3 à 1.6 10-4 °C ~ 0.0002 à 0.002 °C (entre deux millièmes et deux dix millièmes de degré C)
Faut-il en dire plus pour souligner l’ineptie d’une telle initiative, extraordinairement dispendieuse (environ 150 milliards d’euros pour la France, selon la Cour des Comptes), d’autant plus que, dans les faits, malgré les promesses faites publiquement aux COP successives, les plus gros émetteurs de CO2 de la Planète, à savoir les USA, l’Australie et les BRICS (Brésil, Russie, Inde et Chine) n’ont nullement l’intention de réduire leurs émissions; que du contraire, pour les BRICS, afin de soutenir leur développement économique, une motivation somme toute parfaitement légitime et équitable.