2 Les données de base des analyses
2.1 Les séries de température
Généralement, les températures publiées ne sont pas absolues, mais des anomalies de température égales à la différence entre la température absolue et une température moyenne sur une période généralement de 30 ans, préconisée par le WMO (World Meteo Organisation). Tous les 30 ans, les bornes de la période mobile sont adaptées : 1930 - 1960, puis 1960 - 1990, puis 1990 - 2020, etc. Les anomalies de température globale au niveau de la planète sont les moyennes des anomalies locales.
Le site de climate4you offre une bonne discussion des différentes séries de températures (Cliquez sur le bouton “Global Temperature”) .
On y relève par exemple une bonne explication des ajustements subis par les séries de température dont quelques unes sont montrées à la figure Figure 2.1.
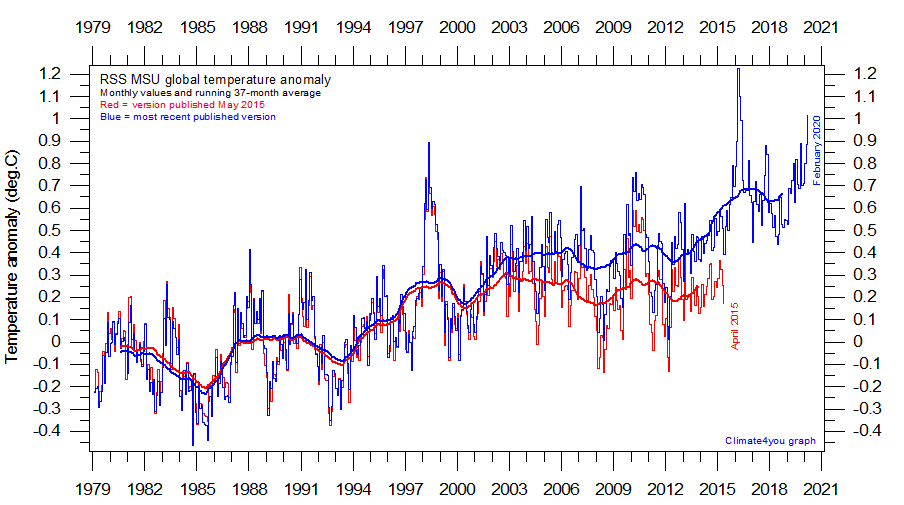
La série rss avant “homogénéisation” n’est pas disponible sur le site de Wood for Trees, mais une comparaison des 2 versions est reprise dans un rapport pdf de septembre 2020 sur le site de climate4you. Voir Figure 2.2.
Les températures relevées par les stations terrestres sont affectées par un effet « d’îlot urbain de chaleur » qui peut être assez important. Dans les séries temporelles non satellitaires, ces relevés terrestres interviennent pour environ 30%.
Dans une étude qui date de 2009, l’IRM estime par exemple que dans la période de 1960 à 1999, 45% de l’élévation de la température moyenne à Bruxelles doit être imputée à l’effet d’îlot urbain de chaleur plutôt qu’à un changement dans le climat local-régional (Hamdi et al. 2009).
Par ailleurs, des effets saisonniers, des phénomènes météos (modification de la couverture nuageuse) ou des phénomènes de courte durée (éruptions volcaniques) peuvent venir perturber les températures « terrestres » beaucoup plus fortement que les températures « océaniques » ; ceci résulte également des différences de capacité thermique existant entre les océans et l’atmosphère.
C’est pour éviter ce genre d’interactions que les séries de températures océaniques (« Hadsst3 data ») (anomalies de températures) et (« Hadisst data ») (températures absolues) ont été retenues dans la présente analyse; celle-ci se focalise donc sur les flux de chaleur radiatifs émis par le soleil, leur absorption par les couches superficielles des océans et les échanges de chaleur (et de matière) océan-atmosphère.
Il convient cependant de savoir que les données les plus anciennes de ces séries proviennent de prélèvements d’eau de surface effectués à partir de navires, forcément uniquement le long des routes commerciales (ce qui pose un problème de représentativité). Plus récemment, cette base de données a été également alimentée par des mesures provenant du réseau de bouées Argo, ce qui a amélioré sa couverture géographique et donc sa représentativité.
Les océans jouent un rôle très important dans la régulation du climat, par leur capacité de stockage de chaleur beaucoup plus importante que celle de l’atmosphère.
2.2 Les taches solaires
La mesure du nombre de taches solaires est une façon simple d’estimer l’activité solaire. Les premières mesures effectuées remontent à 1750. Le nombre de taches solaires passe par un minimum environ tous les 11 ans.
Voir Figure 2.3 et Figure 2.4.
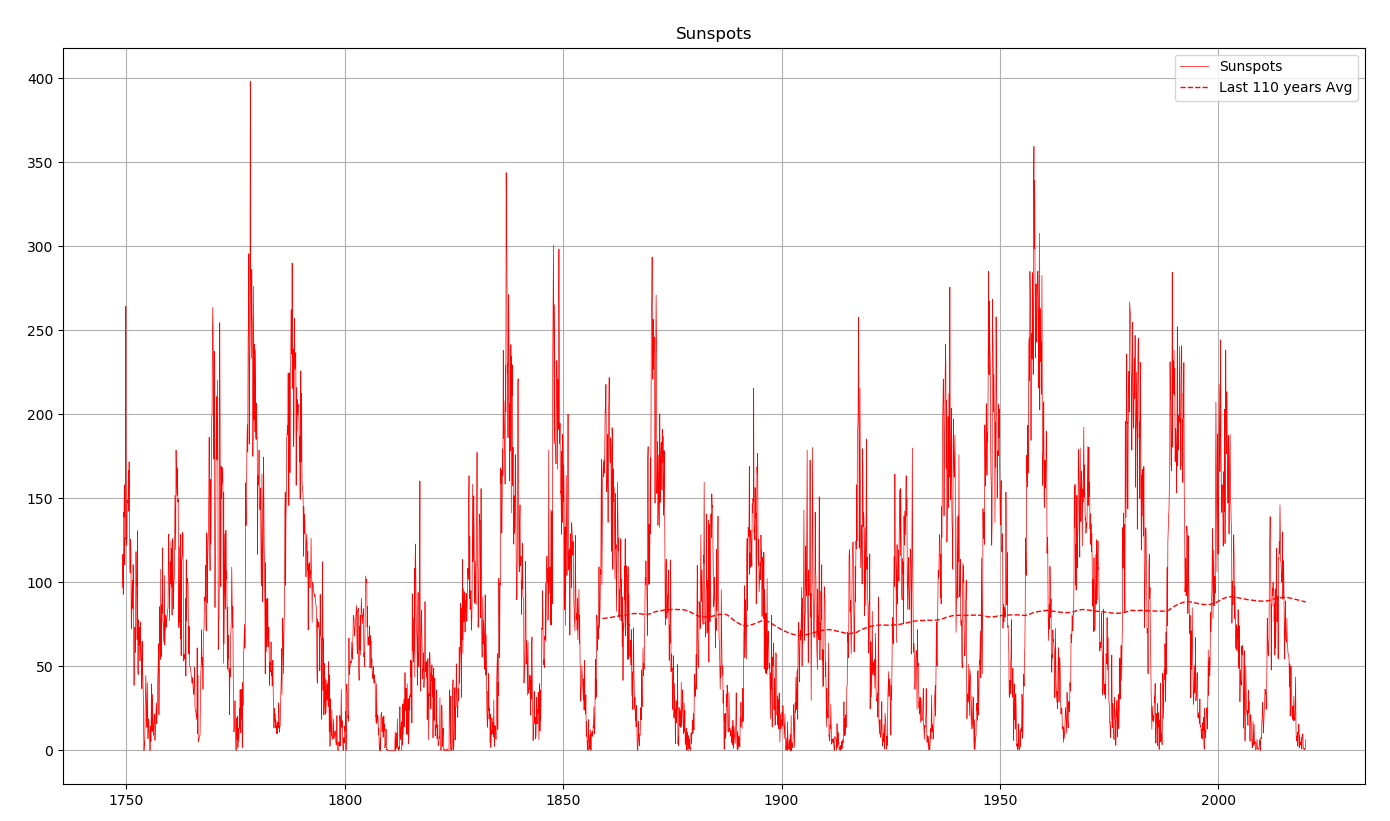
2.3 L’irradiance totale solaire
L’irradiance totale solaire (ITS) est une mesure plus précise de l’activité solaire. L’ITS représente la puissance du rayonnement solaire par unité de surface (W/m2). Elle est mesurée par satellite depuis quelques décennies. La mesure est compliquée. La durée de vie des satellites est limitée, et il y a des problèmes de calibration s’il n’y a pas une période de chevauchement. Cela n’a pas toujours été le cas.
L’ITS peut également être reconstituée par la mesure de marqueurs (10Be et 14C) qui sont corrélés avec le rayonnement solaire. Sur le site du lisird on peut trouver deux reconstructions historiques du rayonnement solaire qui remontent jusqu’en 1610 :
la reconstruction “historical”
la reconstruction “nrl2”
Voir Figure 2.5.
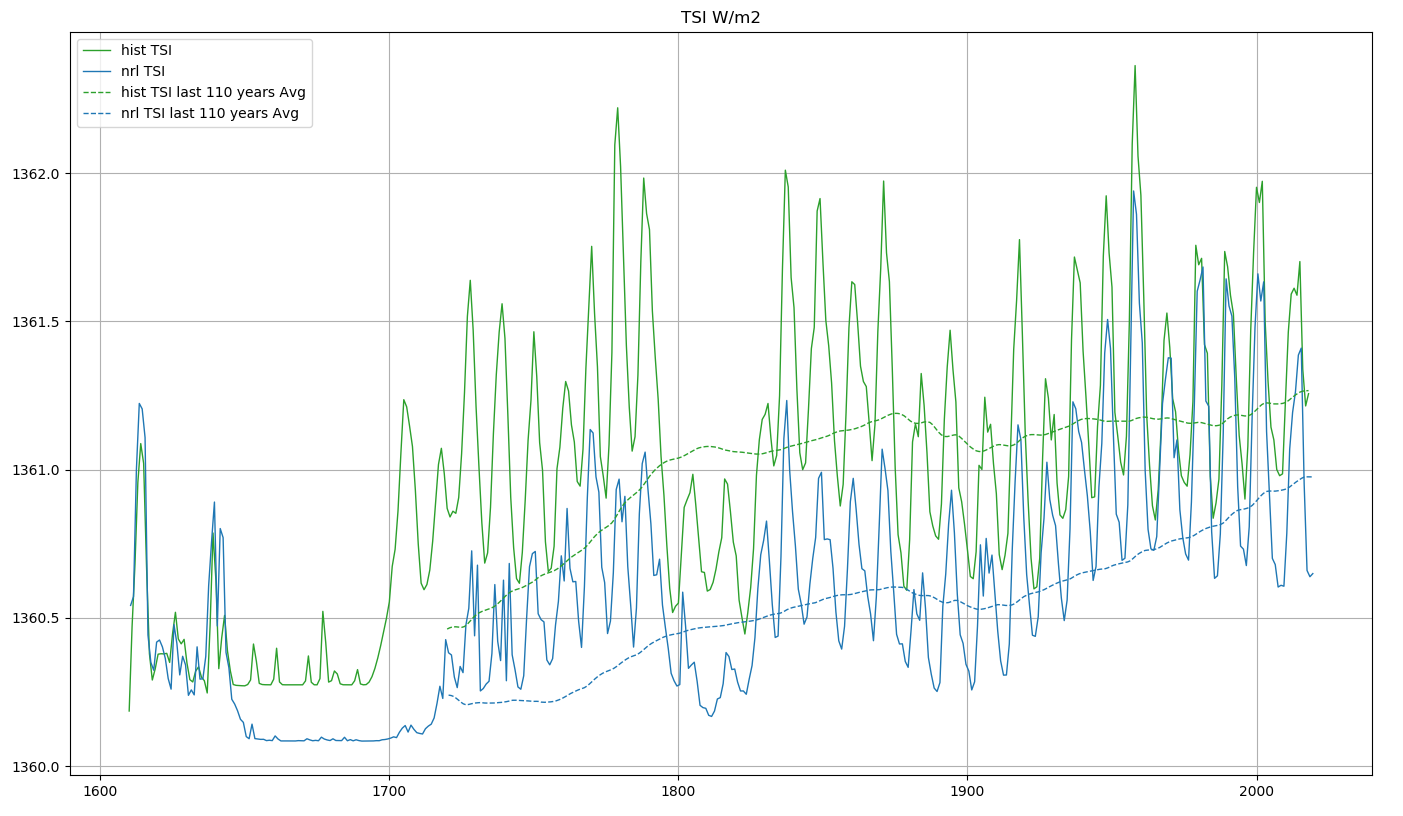
Ces données sont des moyennes annuelles.
Le centre LISIRD de l’Université du Colorado considère que ses reconstructions de l’ITS sont les plus réalistes pour les 400 dernières années.
2.4 La concentration de CO2 atmosphérique
La concentration de CO2 atmosphérique présente une énorme hétérogénéité que révèlent les observations par satellite. Cette vidéo la reflète parfaitement. On ne la retrouve pas dans les relevés terrestres qui présentent une homogénéité étonnante. Voir Figure 2.6.
Le CO2 n’est mesuré avec précision que depuis 1960 dans quelques stations dont la plus connue est celle de Mauna Loa située à Hawaï. Le relevé de Mauna Loa se trouve à cette adresse (« CO
2.4.1 Les modèles du GIEC confrontés aux résultats expérimentaux
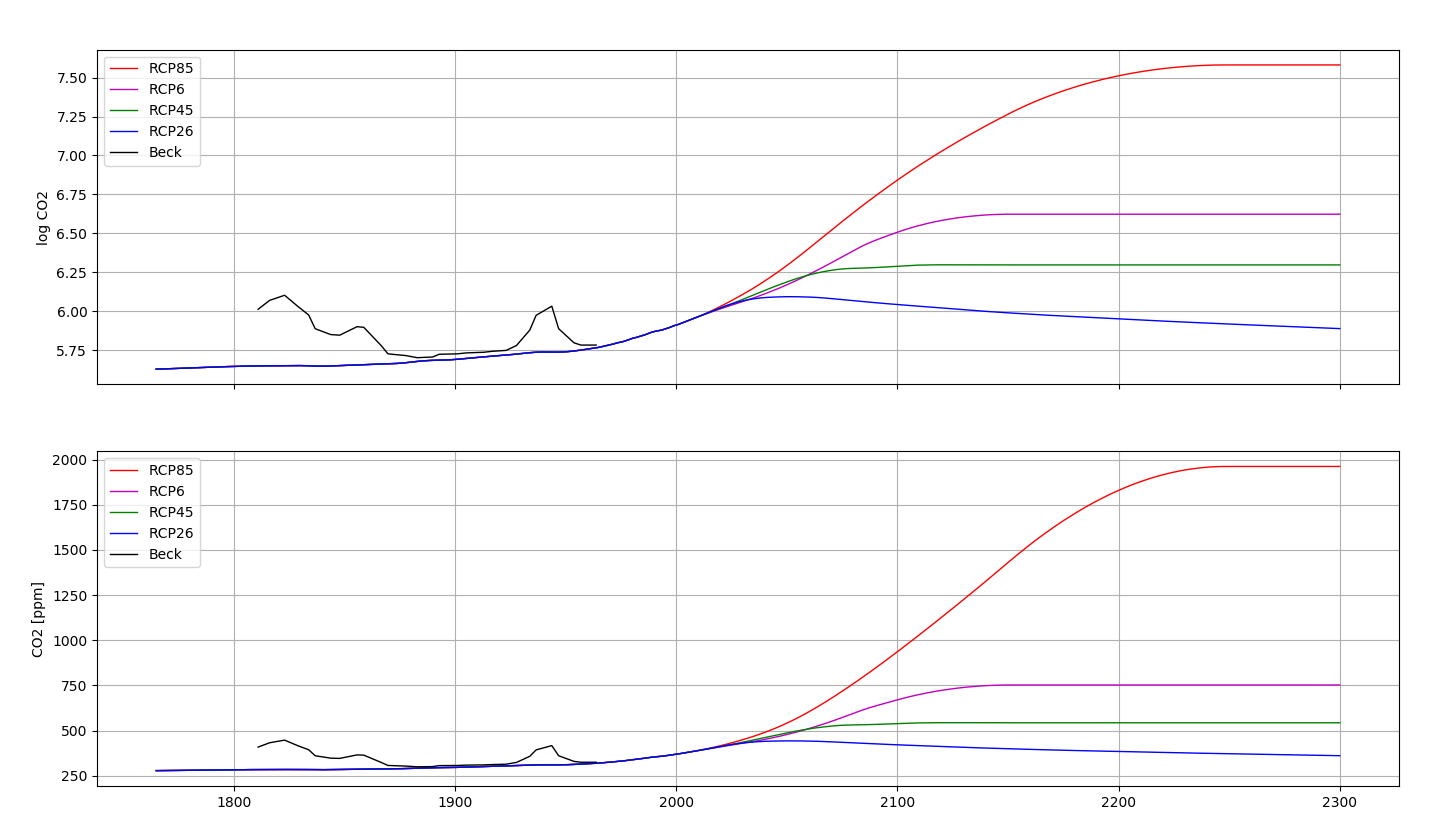
Dans le scénario RCP85, le GIEC fait une projection apocalyptique des concentrations atmosphériques de CO2. Certains se demandent même, après un rapide calcul, s’il y a assez de combustibles fossiles sur Terre pour y arriver.
Ernst-Georg Beck a compilé, pour sa part, 90.000 mesures historiques de CO2 réparties de façon non uniforme sur toute la surface du globe terrestre. (Beck 2007). Il considère que la reconstruction du GIEC est scandaleuse. Voir Figure 2.8.
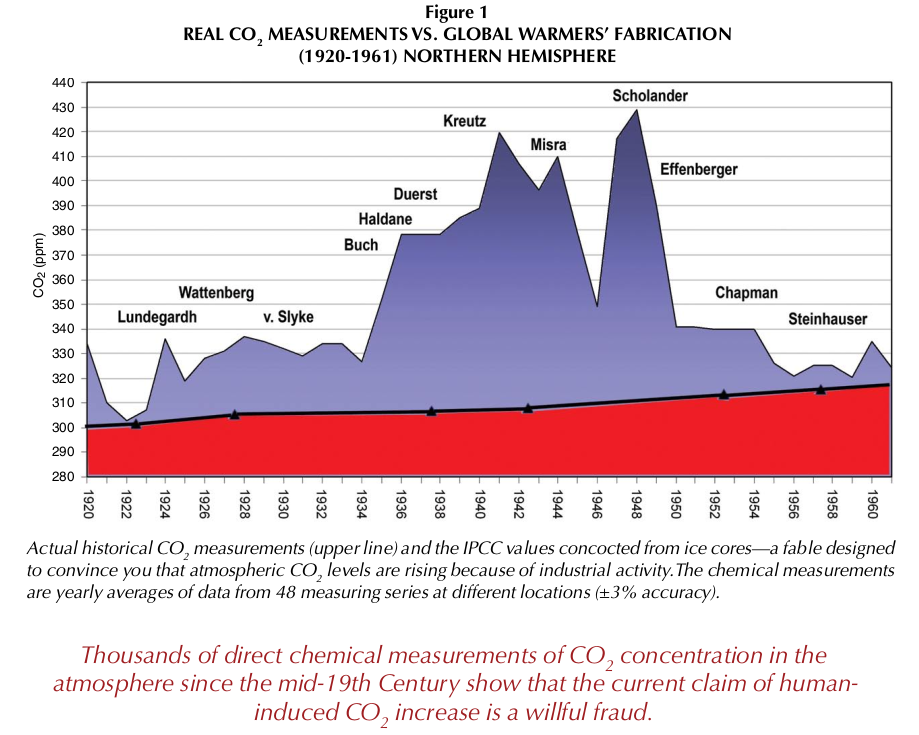
Beck affirme que ses résultats montrent que la concentration de CO2 suit la courbe des températures avec un décalage de 5 ans.
Ceci implique que le CO2 dépend de la température, et pas l’inverse. Si le soleil rentre dans une phase de grand minimum solaire et que les températures diminuent, on pourrait observer un fléchissement ou une diminution du taux de CO2, même si la production anthropique de CO2 continue à augmenter. Ce serait tout à fait incompatible avec les thèses du GIEC.
Par ailleurs les mesures faites sur les carottes glaciaires de Vostök (Petit et al. 1999) montrent que sur plusieurs centaines de milliers d’années, la courbe du CO2 suit à peu près celle de la température, mais avec un décalage d’environ 800 ans, qui ne peut être décelé dans les données discutées précédemment, la fenêtre de mesure que nous prenons en compte qui n’excède pas deux à trois siècles, étant beaucoup trop courte. Il est en effet de bonne pratique en analyse de signaux de ne pas chercher à identifier des cycles dont la période excède un cinquième de la fenêtre de mesure, afin d’éviter les « effets de bord » qui faussent les algorithmes de recherche de périodicité (FFT pour Fast Fourier Transform)
Certains auteurs pensent que cette autre constante de temps serait liée à l’effet d’accumulation-restitution de chaleur par les couches plus profondes des océans.
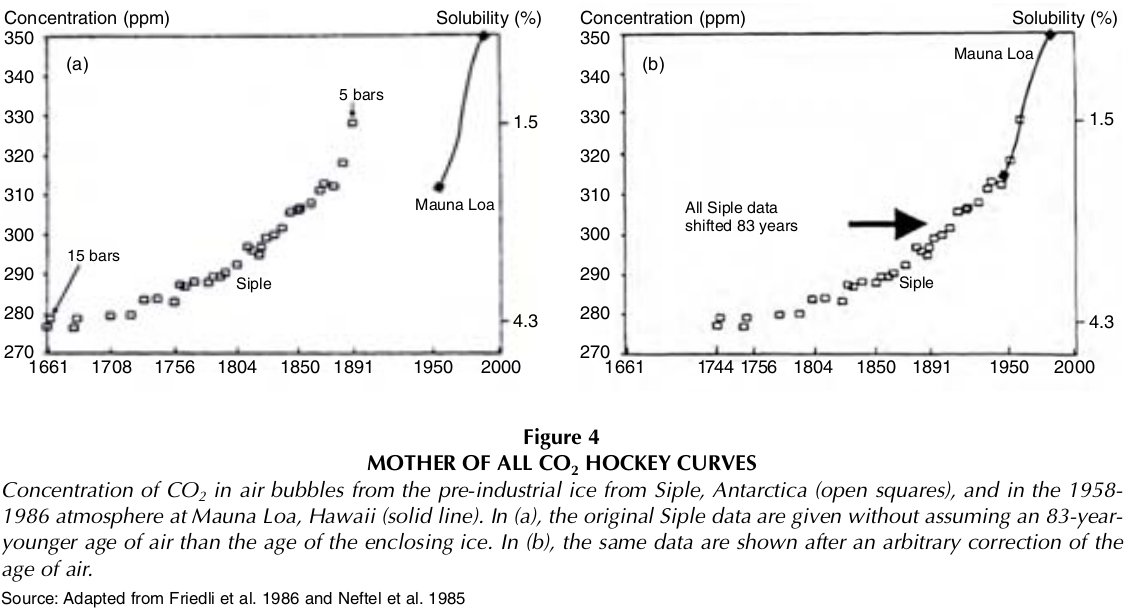
Dans (Jaworowski 2007), l’auteur a violemment protesté contre l’évolution du CO2 selon le GIEC, en expliquant notamment comment le relevé du CO2 des carottes glaciaires a été raccordé aux mesures plus récentes du CO2 atmosphérique à Mauna Loa. Voir Figure 2.9.
Bien que largement accepté, le concept de concentrations de CO2 stables au cours des 11500 dernières années n’est pas supporté par la majorité des estimations de CO2 basées sur les fréquences stomatiques (Wagner et al. 2004).
Le refroidissement d’il y a 8200 ans ne se remarque pas dans les concentrations de CO2 déduites des glaces antarctiques mais apparaît très clairement dans celles déduites des stomates des feuilles fossiles. Voir figure 2 dans (Wagner, Aaby, et Visscher 2002). Cette dernière référence a fait l’objet d’un article (Préat 2019) sur science-climat-energie.
D’après les analyses des fréquences stomatiques au cours du dernier millénaire, le CO2 atmosphérique présente des fluctuations bien plus importantes que ce que l’on déduit des carottes glaciaires. Ces fluctuations sont apparement synchrones avec les changements de température de surface dans l’océan Atlantique Nord (Kouwenberg et al. 2005).
Dans cette intéressante video sur YouTube Carbon Dioxide and Climate Cycles, le professeur David Dilley explique pourquoi le CO2 déduit des carottes glaciaires n’est qu’une moyenne partielle des fluctuations que l’on peut déduire des stomates, et que ces fluctuations sont fortement corrélées à une reconstruction des températures. Il montre qu’il y a eu 6 phases chaudes au cours des 1200 dernières années avec des pics correspondants de CO2, et que l’augmentation du CO2 depuis l’époque préindustrielle est naturelle à 80%. Cette fraction est très proche des 75% que l’on peut déduire d’un calculateur en ligne de la pCO2, basé sur la chimie carbonatée de l’eau de mer (« Calculate ocean pCO2 », s. d.). Ce calculateur a été étudié à la Section 6.2.
2.4.2 L’effet de serre atmosphérique
L’expression de gaz à effet de serre est particulièrement mal choisie. Tout le monde pense la comprendre parce qu’il est bien connu qu’il fait plus chaud dans une serre qu’à l’extérieur. Mais ce n’est pas le même mécanisme qui entre en jeu. La réalité est bien plus complexe.
Dans cet article (Geuskens 2019), le Professeur Geuskens l’explique très bien. Voici ses conclusions:
1. L’effet de serre, qui résulterait de la désactivation radiative (fluorescence) de molécules ayant absorbé une fraction du rayonnement thermique de la Terre, ne peut exister au niveau des basses couches atmosphériques.
2. Au niveau des basses couches atmosphériques, les molécules ayant absorbé une fraction du rayonnement thermique de la Terre se désactivent par collisions avec les molécules environnantes principalement N2 et O2.
3. La conversion d’énergie de vibration des molécules de CO2 en énergie de translation des molécules environnantes ne modifie pas le bilan énergétique global de la Terre.
4. Le CO2 ne peut contribuer en aucune manière à un réchauffement ni de la surface terrestre ni des basses couches atmosphériques.
5. La théorie du réchauffement climatique d’origine anthropique basée sur l’existence d’un effet de serre n’a aucune justification ni théorique ni expérimentale.
Dans cet article très détaillé, (Gerlich et Tscheuschner 2009) il est montré qu’il ne peut y avoir d’effet de serre radiatif, et que cette expression est utilisée à mauvais escient.
Dans le présent travail, un modèle alternatif à celui d’effet de serre atmosphérique est proposé et analysé.
2.5 Fonctions d’auto-corrélation
La fonction d’auto-corrélation est définie par la formule
Cette fonction permet d’identifier
une dérive éventuelle de la série temporelle (ligne de base non horizontale)
le niveau de bruit affectant une série temporelle données, (pic initial – pics périodiques ultérieurs éventuels)/ pics périodiques ultérieurs éventuels),
sa « mémoire » (constante de temps mesurée par la tangente à l’origine)
ses périodicités éventuelles.
2.5.1 Séries de température
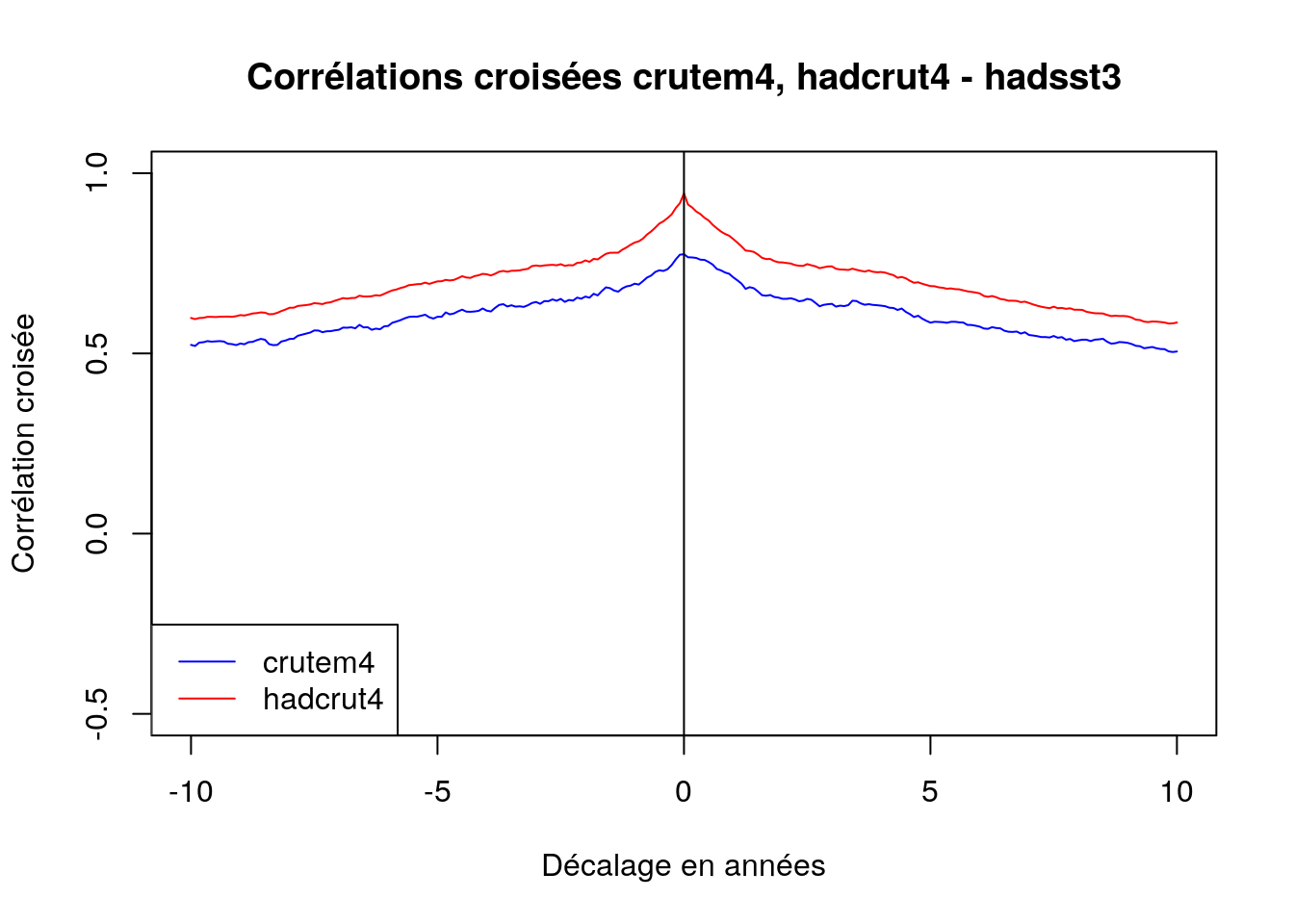
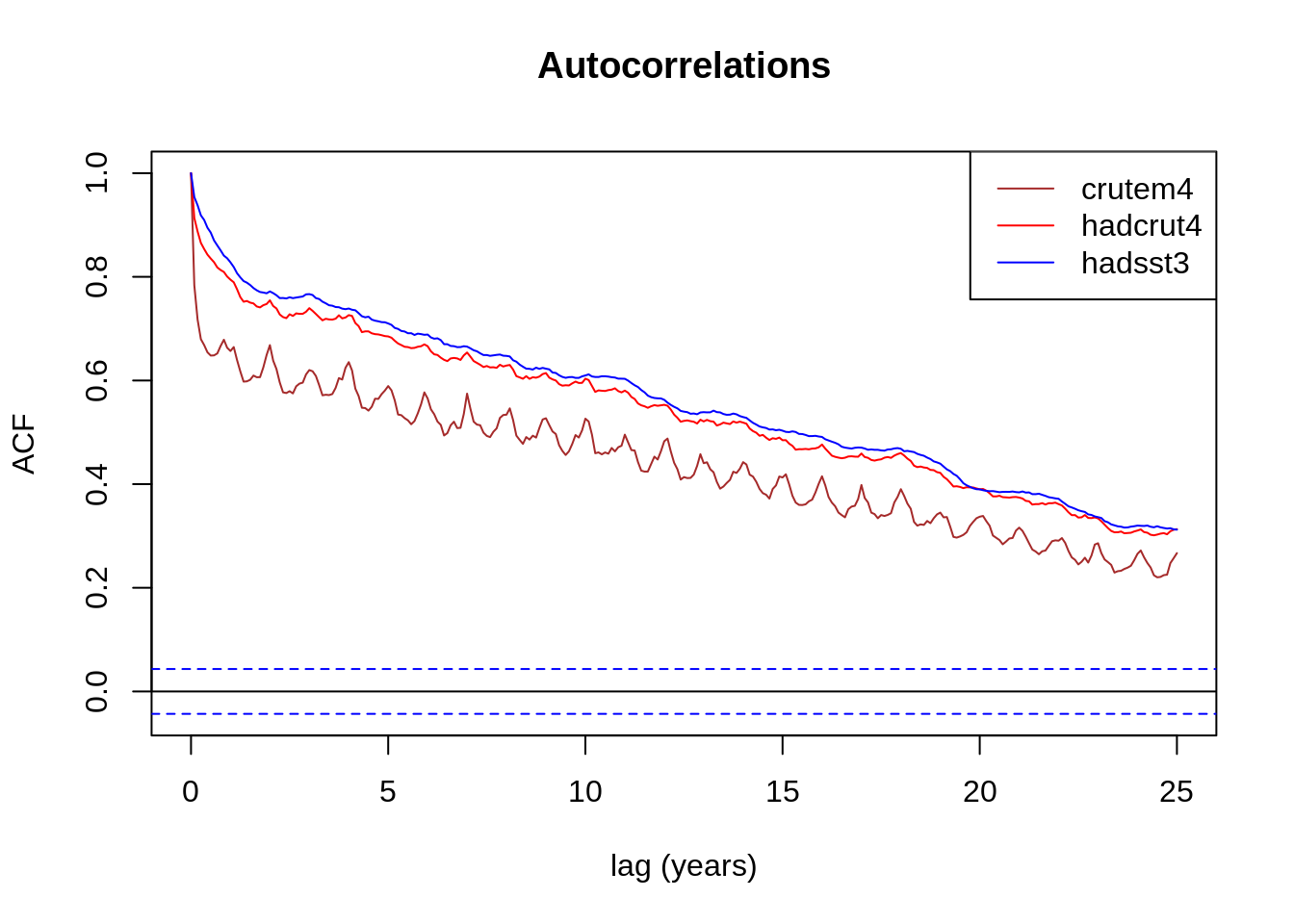
En plus de la série (« Hadsst3 data ») (océans uniquement), les séries (« Crutem4 data ») (terres uniquement) et (« Hadcrut4 data ») (terres et océans) ont également été prises en considération.
Voir figures Figure 2.10 et Figure 2.11.
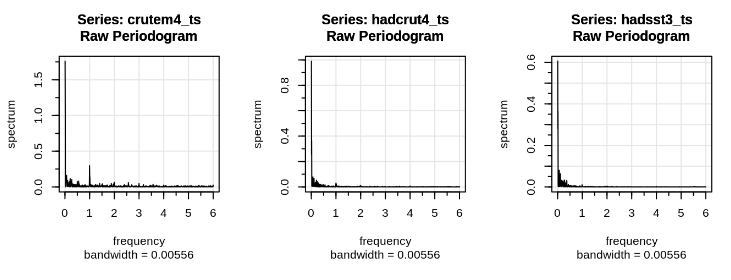
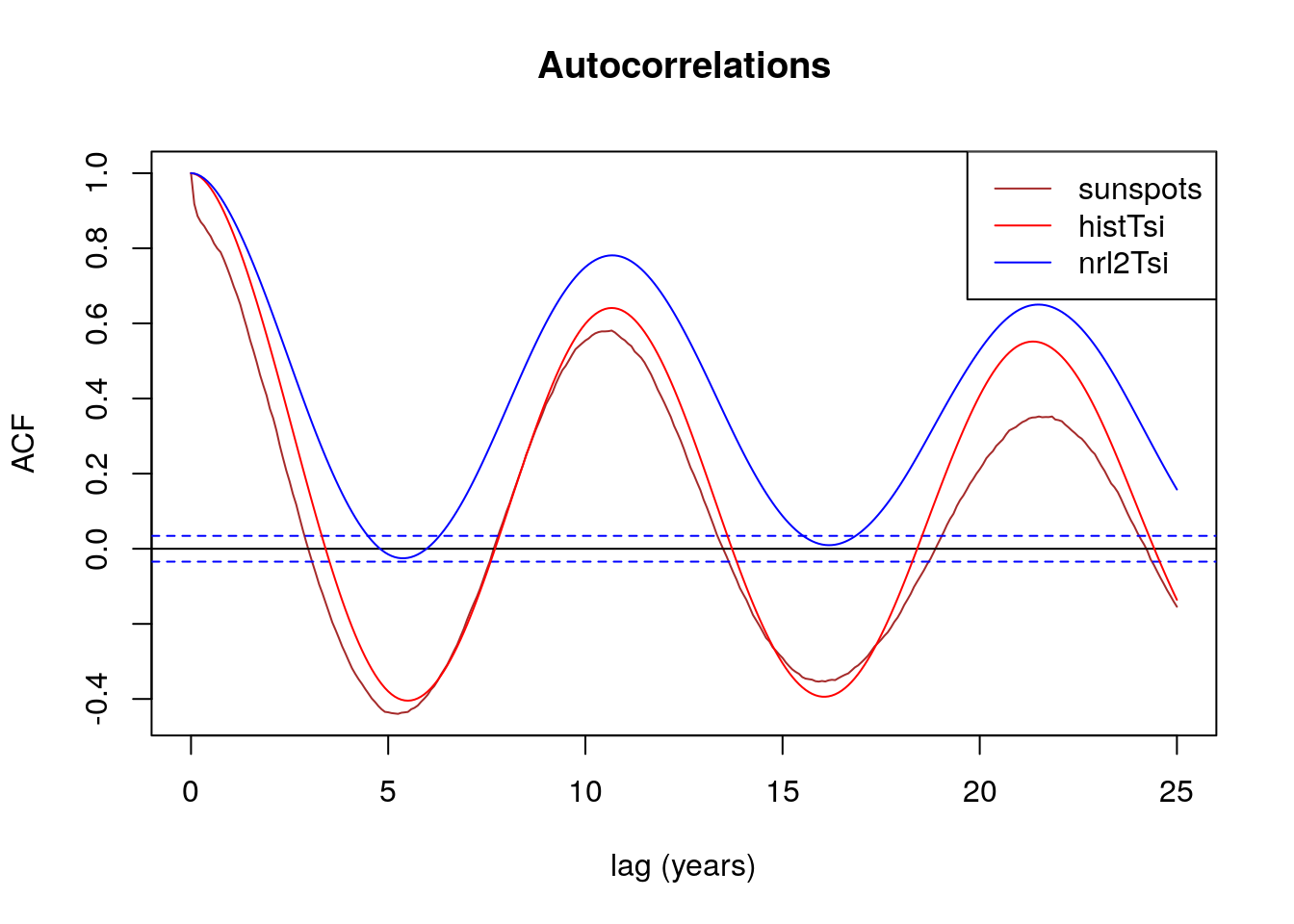
Les séries temporelles de température ont la même allure, révélant une dérive de la ligne de base (signifiant que la température a évolué en fonction du temps). La série hadsst3 « océanique » a une constante de temps (pente à l’origine) plus longue que la série crutem4 « terrestre ». La série crutem4 présente des périodicités saisonnières plus marquées que hadsst3. Ces deux constatations traduisant la plus grande inertie thermique des océans. La série hadcrut4 étant une somme pondérée des deux précédentes, traduit une allure intermédiaire. La série hadsst3 révèle une pseudo-périodicité d’environ 10 ans et une autre d’environ 18 ans. La première est comparable à une périodicité solaire bien connue ; la seconde correspond à l’année lunaire.
Les pics de la fonction d’auto-corrélation sont étalés car les cycles ne sont pas parfaitement périodiques et leur amplitude varie (comme le révèle l’examen des séries temporelles). Ces caractéristiques (modulation d’amplitude et de fréquence) sont souvent observées dans des systèmes légèrement chaotiques (au sens mathématique du terme).
2.5.2 Séries d’activité solaire
2.5.3 Série du CO2 de Mauna Loa
2.6 Examen des relations entre les données de base
2.6.1 Matrices de corrélations
Il est important de ne pas confondre corrélation et causalité. Si deux variables x et y sont corrélées, x peut être la cause de y et/ou y peut être la cause de x, mais il se peut aussi que la relation entre elles soit plus compliquée qu’une causalité simple, ou qu’il n’y ait aucune relation de causalité entre elles.
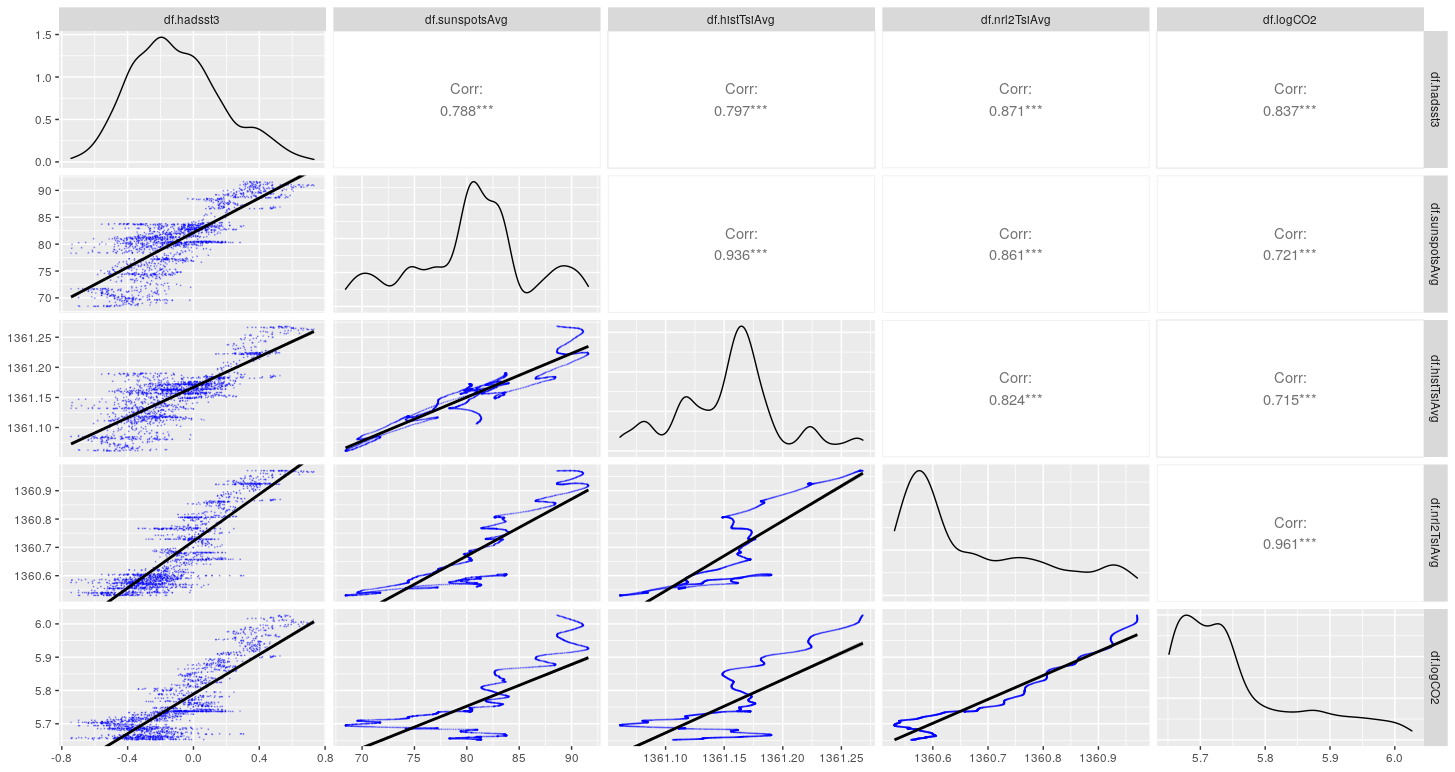
Un moyen très efficace d’évaluer les relations entre des séries est de calculer la corrélation et de tracer le graphe pour chaque paire de séries possible. On obtient une très bonne vue d’ensemble en présentant les résultats sous la forme d’une grille dont la diagonale reprend la densité de la distribution des séries, la partie supérieure droite reprenant les corrélations de chaque paire, et la partie inférieure gauche affichant le graphique de chaque paire.
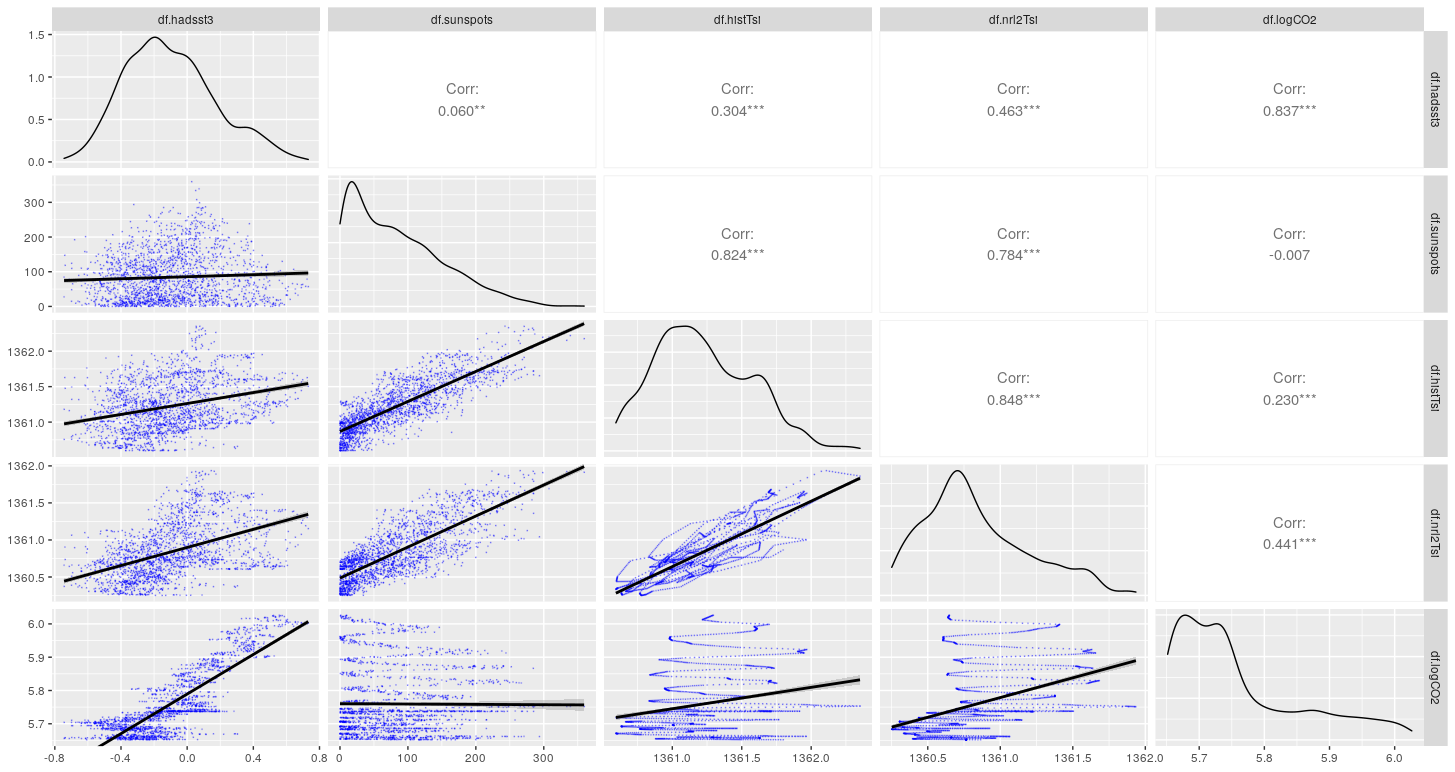
Cette opération a été effectuée pour la température océanique (hadsst3), les taches solaires (sunspots), l’ITS historical (histTsi), l’ITS nrl2 (nrl2Tsi), et le logarithme du CO2 (logCO2). Voir Section 2.6.1.1.
La même analyse a été effectuée avec les activités solaires moyennées sur une période mobile de 110 ans (sunspotsAvg, histTsiAvg, nrl2TsiAvg). Voir Section 2.6.1.2.
2.6.1.1 Relations entre hadsst3, sunspots, histTsi, nrl2Tsi et logCO2
2.6.1.2 Relations entre hadsst3, sunspotsAvg, histTsiAvg, nrl2TsiAvg et logCO2
2.6.2 Analyses de causalité statistique
2.6.2.1 Principes
La fonction de corrélation mesure la dépendance linéaire entre deux séries temporelles X et Y, mais, étant une fonction symétrique, elle ne donne aucune indication concernant laquelle de ces deux séries est une cause de l’autre, ou en d’autres termes, laquelle transfère de l’information vers l’autre. Une chose est certaine, une cause doit toujours précéder, ou à tout le moins être synchrone avec l’effet. Lorsque les deux séries temporelles sont stationnaires (ne présentent pas de tendance en fonction du temps), et qu’elles présentent une dépendance linéaire, la causalité de Granger est la méthode couramment utilisée. Cette méthode repose sur l’idée qu’une variable est la cause d’une autre, si la première des deux contient de l’information améliorant la prédictibilité de l’autre. Le principe de la méthode consiste à prédire Y en se basant sur son histoire propre (ses données antérieures), puis de prédire Y en utilisant à la fois l’histoire de Y et de X, et de comparer ensuite les différences d’ajustement aux données entre ces deux situations, afin de voir si la prise en compte de X améliore la prédiction de Y. En termes mathématiques, l’exercice consiste à mesurer l’erreur d’ajustement
Où
t est le temps
j est le nombre de données du passé utilisées pour effectuer l’ajustement.
On compare ensuite
Afin de vérifier la signification statistique du résultat, on teste alors l’hypothèse que les coefficients de X dans l’équation Équation 2.1 sont tous nuls. A cet effet, on utilise le test de Fisher :
Où:
m est le nombre de restrictions. Dans le cas présent, il s’agit du nombre de coefficients
n est le nombre d’observations historiques prises en compte.
k est le nombre total de paramètres estimés dans le modèle complet Équation 2.1 (constante inclue)
SSEr et SSEu étant respectivement la somme des carrés des écarts pour le modèle incomplet Équation 2.2 et le modèle complet Équation 2.1
Ce faisant, on teste l’hypothèse :
H0: ∀i ∈ {1, . . . , p}, βi = 0,
H1: ∃i ∈ {1, . . . , p}, βi ≠ 0 (au moins un des βi est différent de zéro).
H0 est l’hypothèse que X ne cause pas Y.
La grandeur F de l’ Équation 2.3 suit une distribution de Fisher avec (p, n − 2p − 1) degrés de liberté. Des extensions existent pour traiter les systèmes non linéaires, en utilisant des réseaux neuronaux (méthode VARNN) ; une autre approche consiste à utiliser l’entropie de transfert, basée sur la théorie de l’information, et mesurant le flux d’information de X vers Y (Hmamouche 2020).
D’autres méthodes encore permettent de retrouver les liens de causalité dans des systèmes complexes, à condition que ceux-ci ne présentent pas de boucles de rétroaction (Pearl 2009).
Le présent travail s’est limité à traiter le cas linéaire de la causalité de Granger.
2.6.2.2 Résultats des tests de Granger
La causalité a été testée entre la série hadsst3 et toutes les séries mentionnées à la Section 2.6.1.1 et à la Section 2.6.1.2. La période couverte s’étend de 1850 à nos jours. Toutes les séries ont fait l’objet d’un « detrend » polynomial pour les rendre stationnaires. Un test complémentaire hadsst3_det – logCO2_det a été effectué avec la série du CO2 de Mauna Loa qui est plus précise et qui intègre la variation saisonnière, mais ne remonte que jusqu’en 1958. Voir Table 2.1
| Start year | Source | Destination | crit | lags | p.value |
|---|---|---|---|---|---|
| sunspots | |||||
| 1850 | sunspots_det | hadsst3_det | AIC | 20 | 0.1997184 |
| 1850 | hadsst3_det | sunspots_det | AIC | 20 | 0.2371489 |
| sunspots average | |||||
| 1850 | sunspotsAvg_det | hadsst3_det | AIC | 19 | 0.0000021 |
| 1850 | hadsst3_det | sunspotsAvg_det | AIC | 19 | 0.3087230 |
| histTsi | |||||
| 1850 | histTsi_det | hadsst3_det | AIC | 20 | 0.3797727 |
| 1850 | hadsst3_det | histTsi_det | AIC | 20 | 0.5451372 |
| histTsi average | |||||
| 1850 | histTsiAvg_det | hadsst3_det | AIC | 16 | 0.0000031 |
| 1850 | hadsst3_det | histTsiAvg_det | AIC | 16 | 0.2155396 |
| nrl2Tsi | |||||
| 1850 | nrl2Tsi_det | hadsst3_det | AIC | 14 | 0.6148766 |
| 1850 | hadsst3_det | nrl2Tsi_det | AIC | 14 | 0.9440049 |
| nrl2Tsi average | |||||
| 1850 | nrl2TsiAvg_det | hadsst3_det | AIC | 16 | 0.0000574 |
| 1850 | hadsst3_det | nrl2TsiAvg_det | AIC | 16 | 0.4918525 |
| logCO2 | |||||
| 1850 | logCO2_det | hadsst3_det | AIC | 17 | 0.6688849 |
| 1850 | hadsst3_det | logCO2_det | AIC | 17 | 0.0433063 |
| logCO2 | |||||
| 1958 | logCO2_det | hadsst3_det | AIC | 16 | 0.0004788 |
| 1958 | hadsst3_det | logCO2_det | AIC | 16 | 0.0000000 |
La colonne Start Year est l’année à partir de laquelle les séries sont prises en compte. Les lags ont été calculés selon le critère d’information AIC. D’autres critères ont été évalués et fournissent des résultats analogues non repris ici.
La colonne p.value est la probabilité que l’hypothèse nulle « La Source ne cause pas la Destination » soit fausse. On considère généralement que c’est le cas si la probabilité est inférieure à 0.05.
Aucune causalité n’est détectée entre la température océanique hadsst3 et l’activité solaire non moyennée, quelle qu’elle soit.
Il y a toujours une causalité entre l’activité solaire moyennée, quelle qu’elle soit, et la température océanique. Il n’y a jamais de causalité en sens contraire (heureusement!).
Avec la série complète du logCO2 sans variation saisonnière, qui démarre en 1850, le logCO2 n’est pas la cause de la température océanique, et la température océanique est la cause du logCO2.
Avec la série plus courte du logCO2 de Mauna Loa avec variation saisonnière, la causalité est bidirectionnelle, mais plus marquée dans le sens température océanique => logCO2, que dans le sens inverse. C’est tout à fait logique dans le cadre de l’équilibre de Henry – van ’t Hoff qui est également bidirectionnel. Suivant cet équilibre, l’impact des émissions anthropiques de CO2 sur la température est fort limité. Voir Section 6.2
2.6.3 Corrélations croisées
2.6.3.1 Entre température et activité solaire
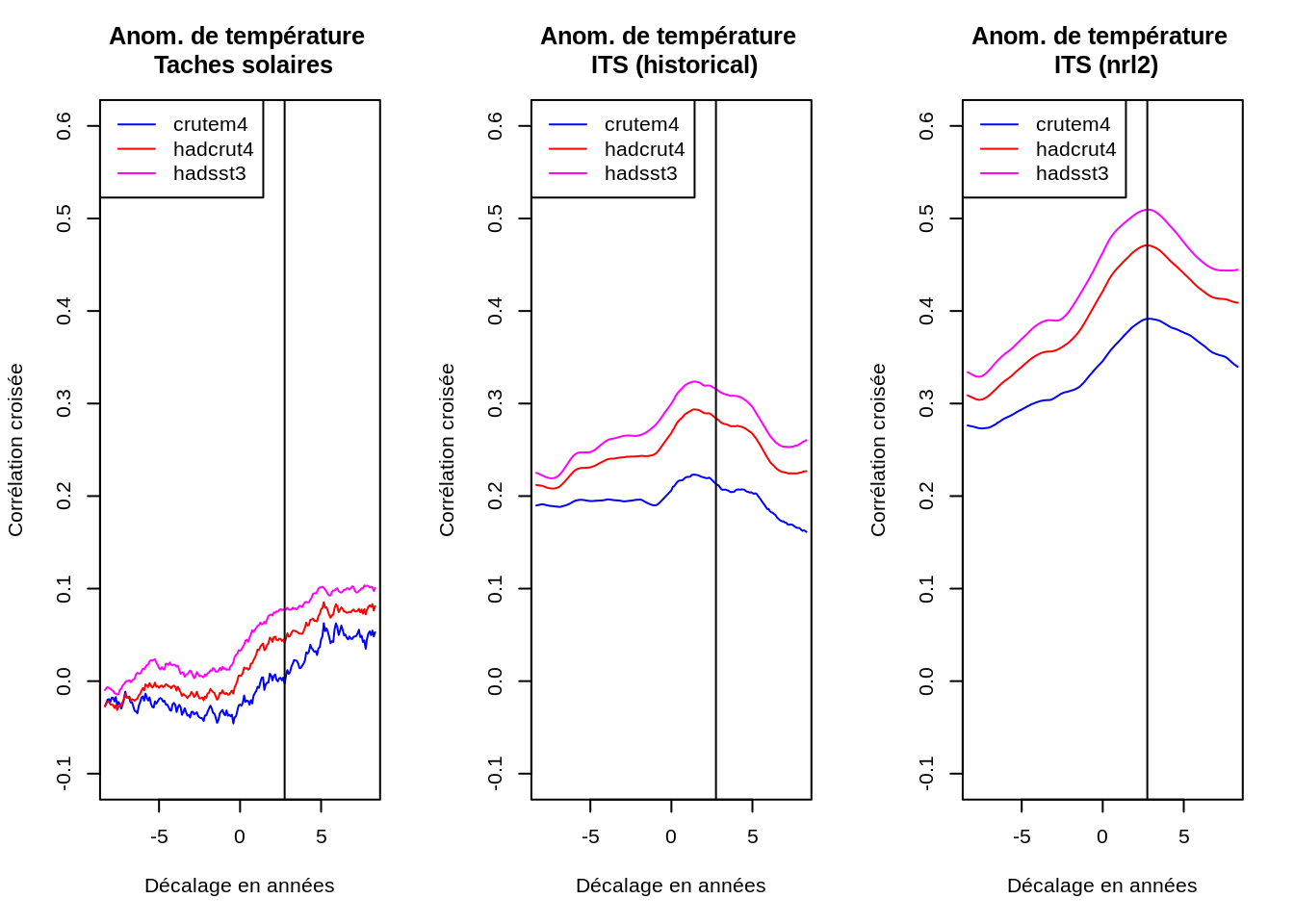
Afin de détecter une relation éventuelle entre température et irradiance, et aussi de choisir les séries temporelles les plus révélatrices, une analyse de corrélation croisée a été réalisée entre diverses données décrivant l’activité solaire et l’anomalie de température.
Le relevé des taches solaires (« Sunspots data »), et l’ITS historical (« LISIRD historical TSI data ») et nrl2 (« LISIRD nrl2 TSI data ») du LISIRD ont été utilisées comme mesure de l’activité solaire.
Pour l’anomalie de température, en plus de la série (« Hadsst3 data ») (océans uniquement), les séries (« Crutem4 data ») (terres uniquement) et (« Hadcrut4 data ») (terres et océans) ont également été prises en considération.
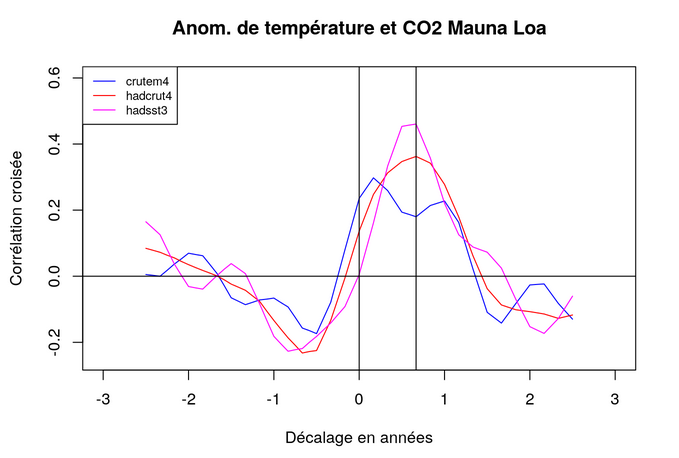
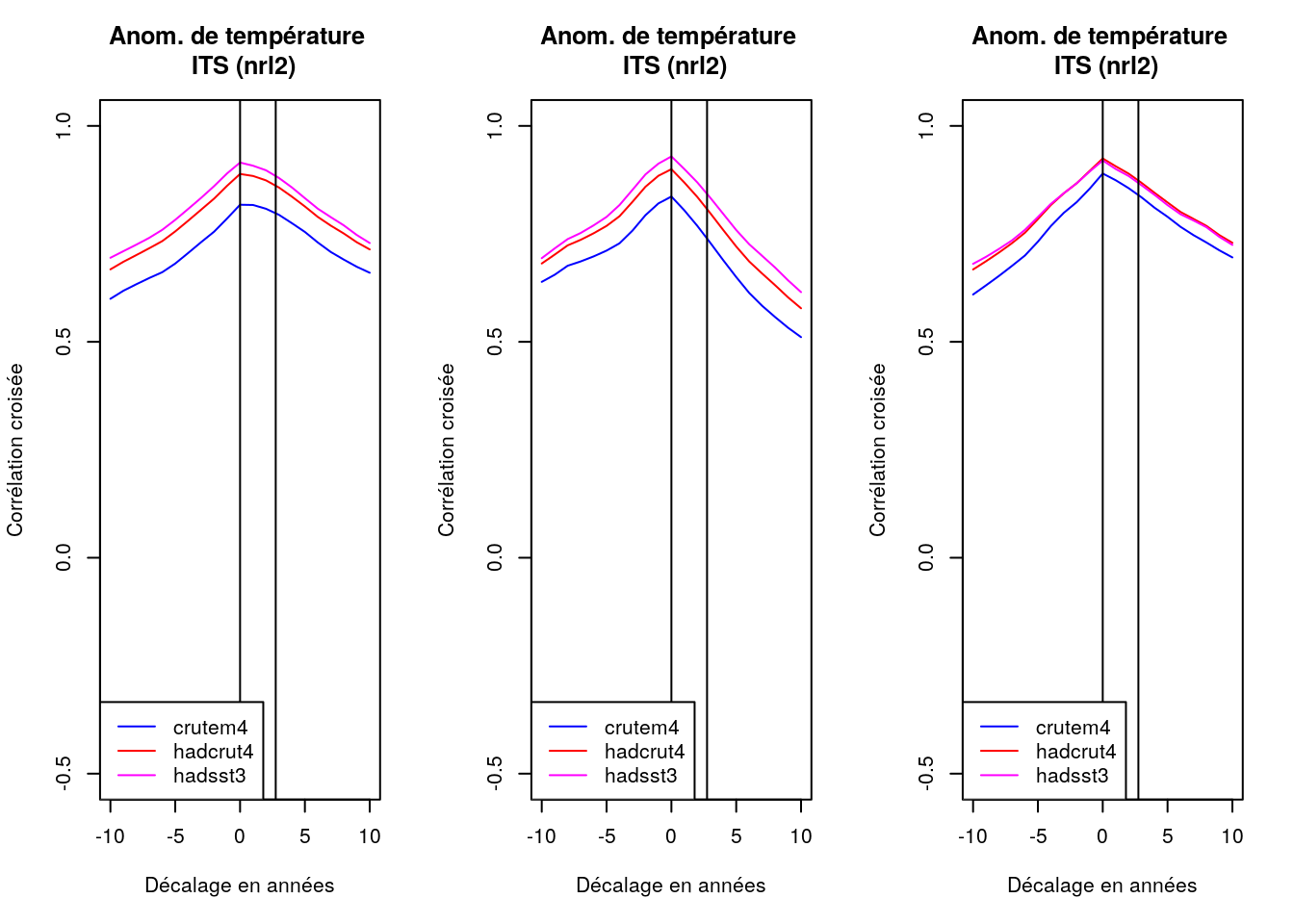
De l’examen de la Figure Figure 2.16, il ressort que quelle que soit la source utilisée pour la mesure de l’activité solaire, la meilleure corrélation croisée est obtenue avec la série océanique hadsst3, et la moins bonne avec la série terrestre crutem4, « contaminée » par des effets parasites, dont l’effet d’ilot urbain de chaleur déjà mentionné ou des changements météo.
Ce résultat incite également à travailler avec l’irradiance plutôt qu’avec le nombre de taches solaires comme indicateur de l’activité solaire, la corrélation croisée étant plus « floue » dans le cas des taches solaires.
Ce décalage de 2.75 ans entre l’irradiance solaire et la température confirme les résultats obtenus par (Stockwell 2011).
Il apparaît donc clairement que la combinaison hadsst3 pour l’anomalie de température et l’ITS nrl2 pour l’activité solaire produit les meilleures corrélations croisées
Cette analyse confirme la corrélation significative entre les fluctuations de température de surface des océans et celles de l’intensité solaire, ainsi que l’antériorité de celle-ci sur les mesures de température. Ce résultat permet donc de conclure que l’intensité solaire remplit deux des conditions nécessaires de causalité (la corrélation et l’antériorité) vis-à-vis de la température « océanique » au sein du système climatique.
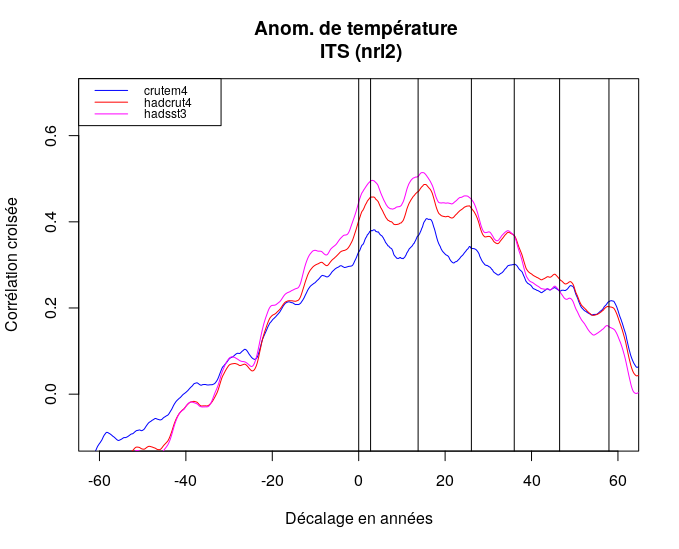
Il est intéressant à ce stade de l’analyse, de se rappeler que l’intégrale d’une sinusoïde est une autre sinusoïde décalée d’un quart de période, et de remarquer que 4*2.75 = 11 ans, ce qui correspond à un cycle solaire bien connu (l’harmonique 2 du cycle de 22 ans d’inversion du champ magnétique solaire). De plus, les durées entre les maxima successifs de corrélation croisée correspondent très bien aux durées des derniers cycles solaires comme le montrent la Figure 2.17 et la Figure 2.18. Ces coïncidences incitent à développer un modèle causal utilisant l’irradiance totale solaire moyennée comme cause des fluctuations de température à la surface des océans.
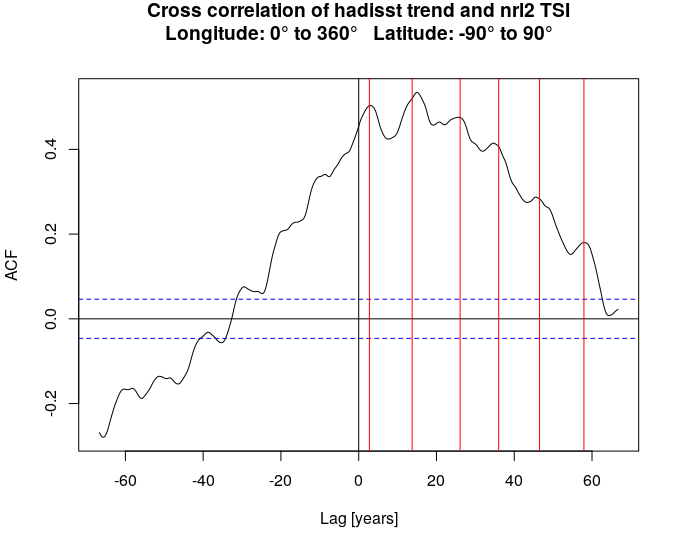
Une analyse complémentaire de corrélation croisée a été effectuée entre la série de températures absolues hadisst et l’irradiance totale solaire nrl2tsi. Voir Figure 2.18.
2.6.3.2 Entre température et activité solaire moyennée
2.6.3.3 Entre température et CO2
En travaillant avec les séries brutes de température et de CO2, on n’observe aucun décalage dans les corrélations croisées. Mais les séries ne sont pas stationnaires. La situation change complètement lorsqu’on les rend stationnaires par différentiation. Le CO2 suit la température avec un décalage de 8 mois. Voir Figure 2.20. Une cause devant précéder ou être synchrone avec son effet, la variation de CO2 ne peut être la cause de la variation de température.
La variation saisonnière a été éliminée du relevé du CO2 avant d’effectuer la différentiation. Cette procédure de calcul rejoint la technique du DIFF12 décrite dans (Humlum, Stordahl, et Solheim 2013) où un décalage analogue a été rapporté.