4 Une modélisation simple de l’anomalie de température globale en fonction du rayonnement solaire
Symboles utilisés dans les formules
| Le temps | |
| L’anomalie de température au temps |
|
| Un coefficient | |
| Une durée correspondant à l’inertie thermique des océans | |
| Le rayonnement solaire moyen entre le temps |
|
| Un rayonnement solaire de référence. | |
| Le rayonnement solaire au temps |
4.1 Un modèle statique
L’approche classique et statique peut s’exprimer comme suit:
Elle suppose que l’équilibre thermique s’établit instantanément. Cette approche produit de très mauvaises corrélations et ne peut expliquer que de très faibles variations de température. Voir Figure 4.1.
4.2 Un modèle dynamique
En remplaçant le rayonnement solaire instantané par le rayonnement solaire moyen des
Utiliser le rayonnement solaire moyen des
Dans ce modèle, la planète est perpétuellement en état de déséquilibre thermique. (Abdussamatov 2013) a bien décrit les mécanismes physiques responsables de ce déséquilibre.
L’anomalie de température est nulle lorsque le rayonnement solaire moyen est égal au rayonnement solaire de référence. Lorsque le rayonnement solaire moyen est supérieur au rayonnement solaire de référence, l’anomalie de température est positive. Elle est négative dans le cas contraire.
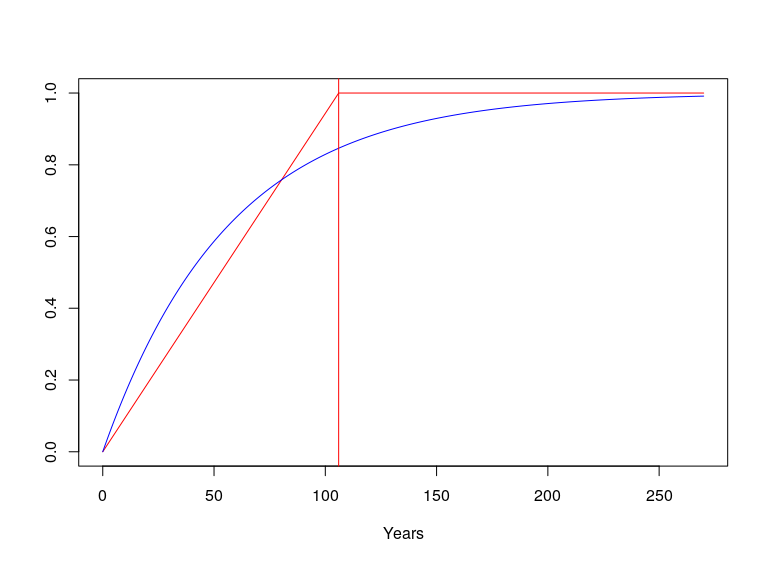
La température ne se stabilise que si le rayonnement solaire reste constant pendant
Une parenthèse: l’océan comme volant d’inertie
Si dans l’Équation 4.2 on remplace
par , par , par et par , on obtient l’équation du mouvement d’un volant d’inertie rotationnelle soumis à un couple moteur et à un couple résistant :
L’équation qui lie l’anomalie de température et le rayonnement solaire est donc analogue à celle qui décrit l’accélération angulaire d’un volant d’inertie.
Lorsqu’on utilise l’Équation 4.2 dans une analyse de régression, l’examen des résidus révèle la présence d’un terme harmonique, indépendant du rayonnement solaire, et qui pourrait résulter des boucles convectives verticales et horizontales (les « courants », le « conveyor belt », le gulf stream, les phénomènes NAO, PDO, etc.) existant au sein des océans et circulant respectivement entre couches superficielles et profondes, ou entre zones chaudes et froides; et dont on détecte la trace de la composante principale dans les résidus. En l’ajoutant à l’Équation 4.2 , on obtient :
Dans cette expression,
| représente l’amplitude, | |
| la période et | |
| la phase de l’oscillation |
Les analyses de régression multiple effectuées optimisent tous les paramètres de l’Équation 4.2 ou de l’Équation 4.3 par une technique classique de minimisation des moindres carrés, les équations non linéaires étant résolues en optimisant des itérations successives.
Pour quantifier le rayonnement solaire on peut utiliser le nombre de taches solaires ou l’irradiance totale solaire (ITS).
4.3 Un modèle thermique équivalent au modèle dynamique
Il est intéressant de noter que la modélisation de l’anomalie de température par une moyenne du rayonnement solaire n’est qu’une autre formulation du modèle thermique utilisé par Stockwell et exposé dans un de ses autres articles (Stockwell 2011) :
Dans ce modèle,
Cette hypothèse semble bizarre à première vue, la contribution radiative comprenant normalement un terme en T4 . Cette formule correspond cependant à une démarche relativement courante, lorsqu’on travaille aux environs de la température ambiante. Voir (McCabe, Smith, et Harriott 1993).
Elle revient à considérer que le terme radiatif est un complément au coefficient de transfert convectif hc, la formule de transfert de chaleur combinée radiative-convective devenant :
Dans ces formules :
| masse spécifique [kg/m3] | |
| chaleur spécifique [Joules /(kg°K)] | |
| température [°K] | |
| temps (h) | |
| coefficient de transfert convectif (empirique) [W/(m2 °K)] | |
| coefficient de transfert radiatif “linéarisé” [W/(m2°K)] | |
| surface d’échange [m2] | |
| température de l’autre milieu avec lequel la chaleur est échangée [°K] | |
| la constante de Stefan-Boltzmann [ |
|
| l’émissivité [0] |
Moyennant cette linéarisation, obtient alors
Posons
Si l’on considère
Dans cette formule,
Si
Après une longue période, la variation de température se stabilise :
Si l’on discrétise la fonction S(t) en plusieurs escaliers, en la supposant constante dans les intervalles i, i+1 on obtient
Si l’on approche
la formule peut alors s’écrire sous forme de différences finies
Avec
En développant les sommes et en regroupant les termes , on obtient facilement
avec
Il vient finalement
Ce qui est tout à fait équivalent à l’Équation 4.2 introduite à la Section 4.2.
Remarquons au passage que
Dans le cas où
En remplaçant
La variation de température est un signal sinusoïdal dont l’amplitude vaut
et qui est déphasée d’un angle
Pour des oscillations lentes,
Pour des oscillations rapides,
4.4 Estimation des valeurs numériques des paramètres du modèle thermique
L’analyse TS.5 (voir Section 4.7.6) fournit directement la valeur de
Le coefficient k peut également être trouvé en résolvant l’Équation 4.15 par rapport à k :
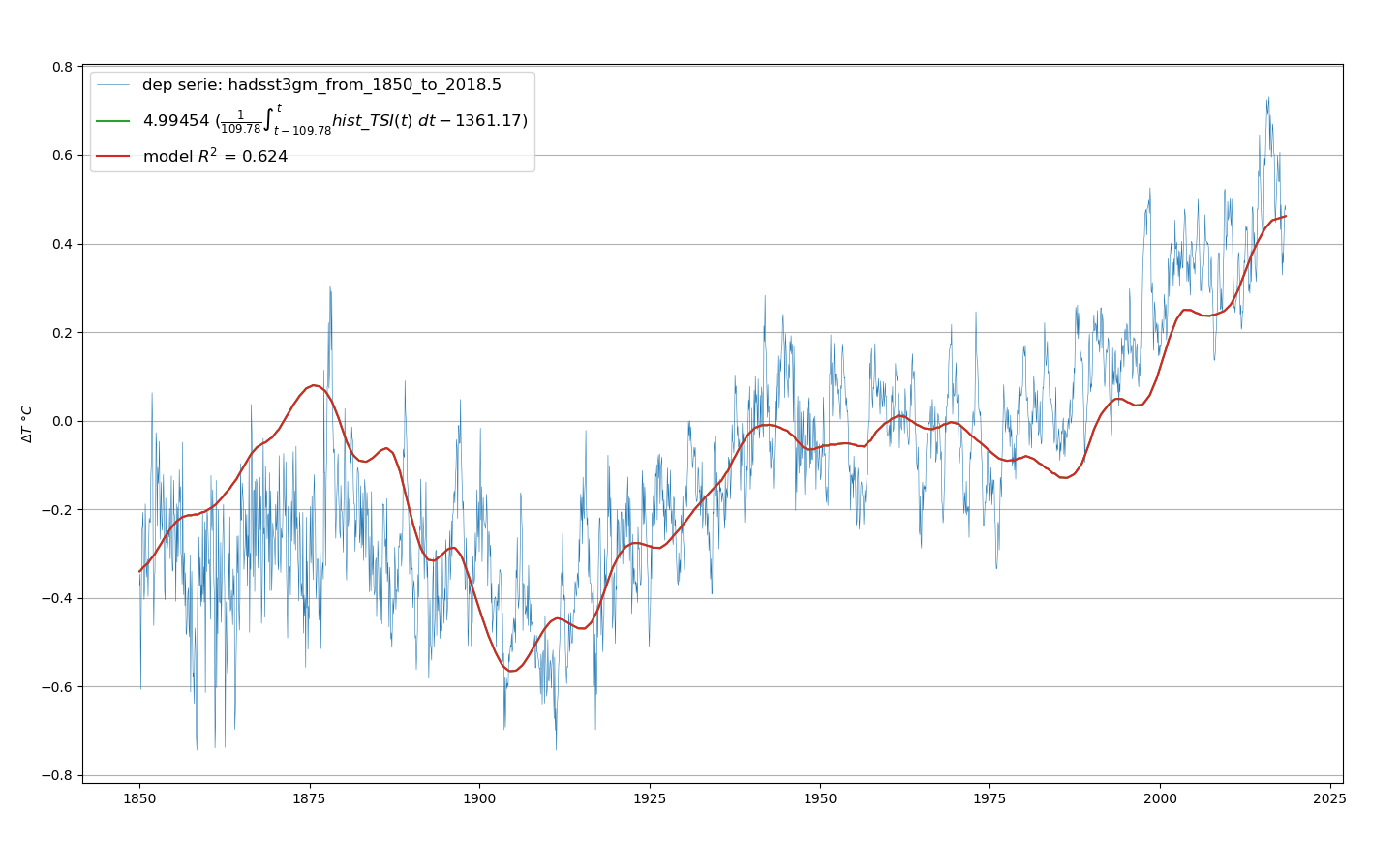
L’examen des ondulations de la courbe rouge de la Figure 4.27 autour des années 1960 permet d’estimer pour un cycle solaire de 11 ans,
Avec
Avec k=56.6 ans, le déphasage du cycle solaire par rapport au rayonnement est donné par l’Équation 4.17, et vaut 88.2 degrés.
Ceci confirme le décalage d’un quart de période entre la température et l’activité solaire (voir Figure 2.16) et valide donc également l’analogie de l’océan avec un filtre passe-bas « intégrateur ».
Avec
Pour un rayonnement sinusoïdal
| 1 | 11 | 100 | 200 | 500 | 1000 | 10000 | year | |
| 6.2832 | 0.5712 | 0.0628 | 0.0314 | 0.0126 | 0.0063 | 0.000063 | 1/year | |
| 0.0047 | 0.0513 | 0.4494 | 0.8137 | 1.3527 | 1.5640 | 1.6600 | °K | |
| 89.8 | 88.2 | 74.3 | 60.6 | 35.4 | 19.6 | 0.2 | angular ° | |
| 0.25 | 2.70 | 20.64 | 33.69 | 49.20 | 54.38 | 56.60 | year |
L’amplitude de la variation de température est faible lorsque la période est courte, et tend vers la valeur correspondant à une variation constante du rayonnement solaire lorsque la période est très longue. Le déphasage passe progressivement de 90 degrés vers 0 degré. Pour une même variation de rayonnement solaire, la variation de température est environ 16 fois plus forte pour une période de 200 ans que pour une période de 11 ans. Les différences de température entre les valeurs max et min sont égales au double des valeurs mentionnées. Par exemple, pour un cycle de 200 ans, la variation totale de température est de 1.6 °K.
4.5 Analogie du modèle thermique avec un circuit électrique de type RC
L’Équation 4.7 est équivalente à celle qui décrit le fonctionnement d’un circuit électrique de type RC. Voir ici.
La différence de potentiel aux bornes du condensateur est donnée par l’équation suivante :
L’équivalence des symboles des 2 équations est donnée par la table suivante :
| Modèle thermique | Circuit RC |
|---|---|
4.6 Rayonnement solaire, températures et anomalies de température
On considère souvent que la température étant une grandeur intensive qui n’a qu’une signification thermodynamique locale, moyenner spatialement des températures locales n’a pas de sens, et qu’il faudrait par conséquent se limiter à ne faire que des analyses climatiques locales.
Nous allons voir que ce n’est pas le cas pour les températures de surface océanique : le modèle thermique décrit précédemment explique à la fois les températures et leurs anomalies.
Il se fait qu’en moyenne, à chaque latitude, on peut définir une anomalie de température locale qui est proportionnelle au rayonnement solaire incident local qui ne dépend également que de la latitude.
Ces anomalies de températures locales peuvent dès lors être moyennées spatialement pour en dériver une anomalie de température globale qui est proportionnelle au rayonnement solaire global au sommet de l’atmosphère qui n’est autre que l’irradiance totale solaire.
Les analyses suivantes sont basées sur la série hadisst du Met Office – Hadley Centre. Les données peuvent être téléchargées ici (« Hadisst data »).
Cette série reprend pour chaque mois depuis 1870 les températures de surface océanique pour un maillage en latitude et en longitude de 1° x 1° , soit 64800 points par mois, et plus de 100 millions de données au total.
4.6.1 Principes des calculs
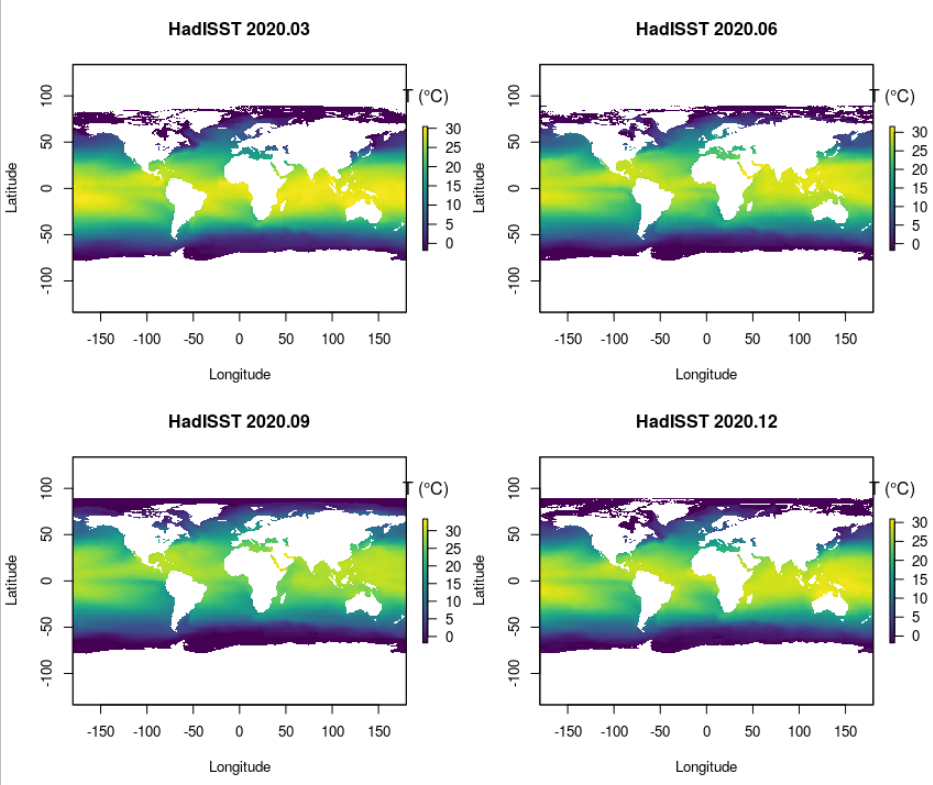
Les températures de surface océaniques sont relativement homogènes à une latitude donnée, quelle que soit la saison. Il y a quand même plusieurs exceptions :
l’Atlantique Nord est plus chaud que le Pacifique Nord
au Sud de l’équateur, les côtes Est de l’Afrique et de l’Amérique du Sud sont plus chaudes que les côtes Ouest
les phénomènes El Niño – La Niña induisent des perturbations.
Il y a une variation saisonnière, mais aux niveaux de l’équateur et des cercles polaires, les températures sont assez stables. Voir Figure 4.4.
Cette distribution des températures n’est pas sans rappeler celle du rayonnement solaire incident à la surface de la planète qui présente également un maximum au niveau de l’équateur, et des minima dans les zones polaires.
Le rayonnement solaire incident a été calculé pour chacun des 64800 points de la surface de la planète, toutes les 10 minutes pour une année complète, avec des moyennes par jour, par mois et pour l’année entière. On considérera que l’orbite de la planète est suffisamment stable entre 1870 et nos jours pour que la comparaison avec n’importe quelle période ou année de la série hadisst soit valide.
Il faut appliquer un flag ( 1=océan ou 0=terres) pour ne garder que les points correspondants aux océans. Ce flag est déduit de la série hadisst pour chaque mois. Dans la série hadisst, la banquise est en effet affectée d’une température conventionnelle égale à -1000 °C qui doit être ignorée pour ne pas fausser les calculs. La banquise évoluant au fil des saisons et des années, cette information n’est évidemment pas constante. Les terres quant à elles, ont une température égale à NA (not available) qui doit également être ignorée. Cela peut éventuellement être le cas aussi pour des données manquantes.
Pour chaque mois analysé, les températures et le rayonnement solaire incident ont été moyennés par latitude et comparés par analyse de régression.
La température moyenne globale a également été calculée pour chaque mois. Elle a fait l’objet de quelques analyses statistiques et été comparée avec la série mensuelle hadsst3.
4.6.2 Températures globales hadisst et comparaison avec les anomalies de température de la série hadsst3
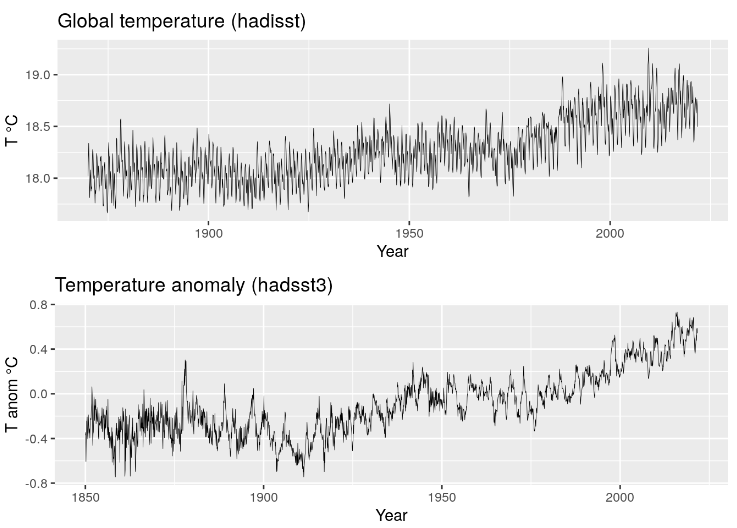
La température moyenne globale de la série hadisst a été calculée en moyennant les 64800 mesures mensuelles pondérées par le cosinus de leur latitude. Son graphe est repris à la Figure 4.5 qui présente également celui de la série hadsst3 à titre de comparaison.
Les deux graphiques sont superposés dans la Figure 4.6, après ajout à la série hadsst3 de la température moyenne de la série hadisst au cours de la période de référence (1961 – 1990).
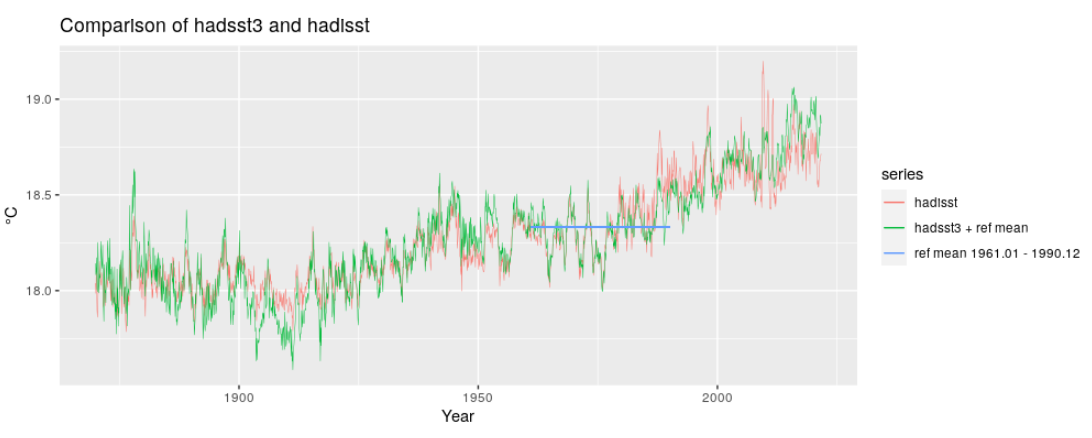
Afin d’affiner la comparaison, les deux séries ont fait l’objet d’une décomposition additive en termes de tendance (trend), de variation saisonnière (seasonal) et le reste (remainder). Voir Figure 4.7 et Figure 4.8.
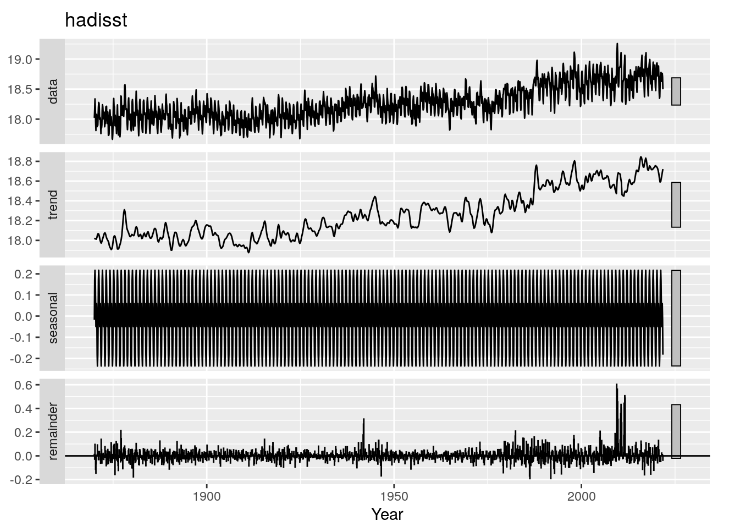
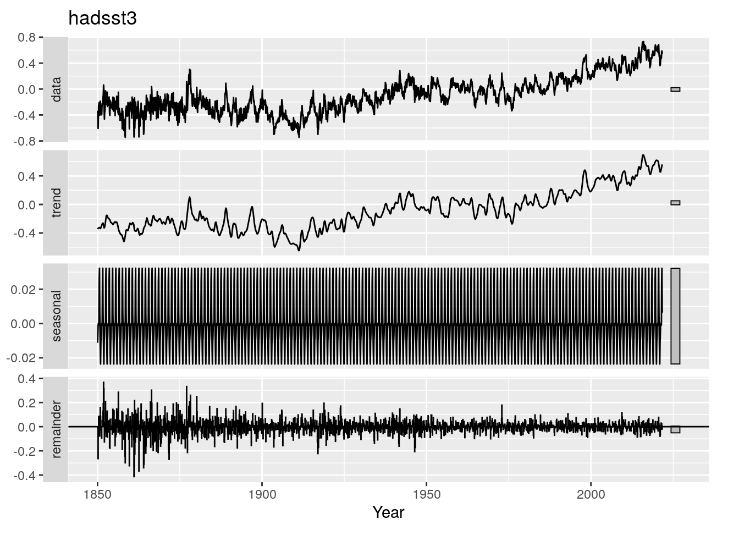
4.6.3 Le rayonnement solaire incident
La Terre tourne autour du Soleil en parcourant en 365.25 jours une orbite elliptique dont le soleil occupe un des foyers. La distance moyenne Terre – Soleil définit l’unité astronomique (1 UA = 1.496 108 km). Elle passe par un maximum au cours de l’été de l’hémisphère Nord, et par un minimum au cours de l’hiver de l’hémisphère Nord. Voir Figure 4.9.
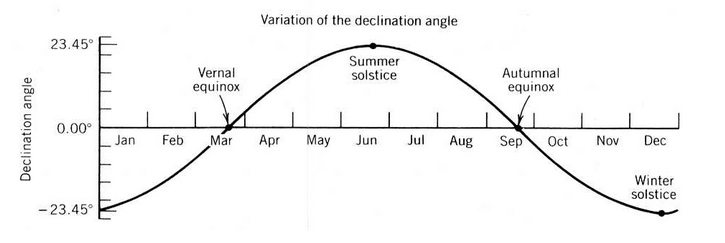
L’altitude aussi appelée élévation du soleil en un point de la surface terrestre est l’angle entre la direction du soleil et le plan horizontal local. Le rayonnement solaire en ce point est proportionnel au sinus de l’altitude, en tenant compte du fait que le soleil est sous l’horizon lorsque l’altitude est négative, et que dans ce cas, le rayonnement incident est bien évidemment nul. Voir Figure 4.10.
Quelques exemples de trajectoires du Soleil sur la sphère céleste sont affichés à la Figure 4.11.
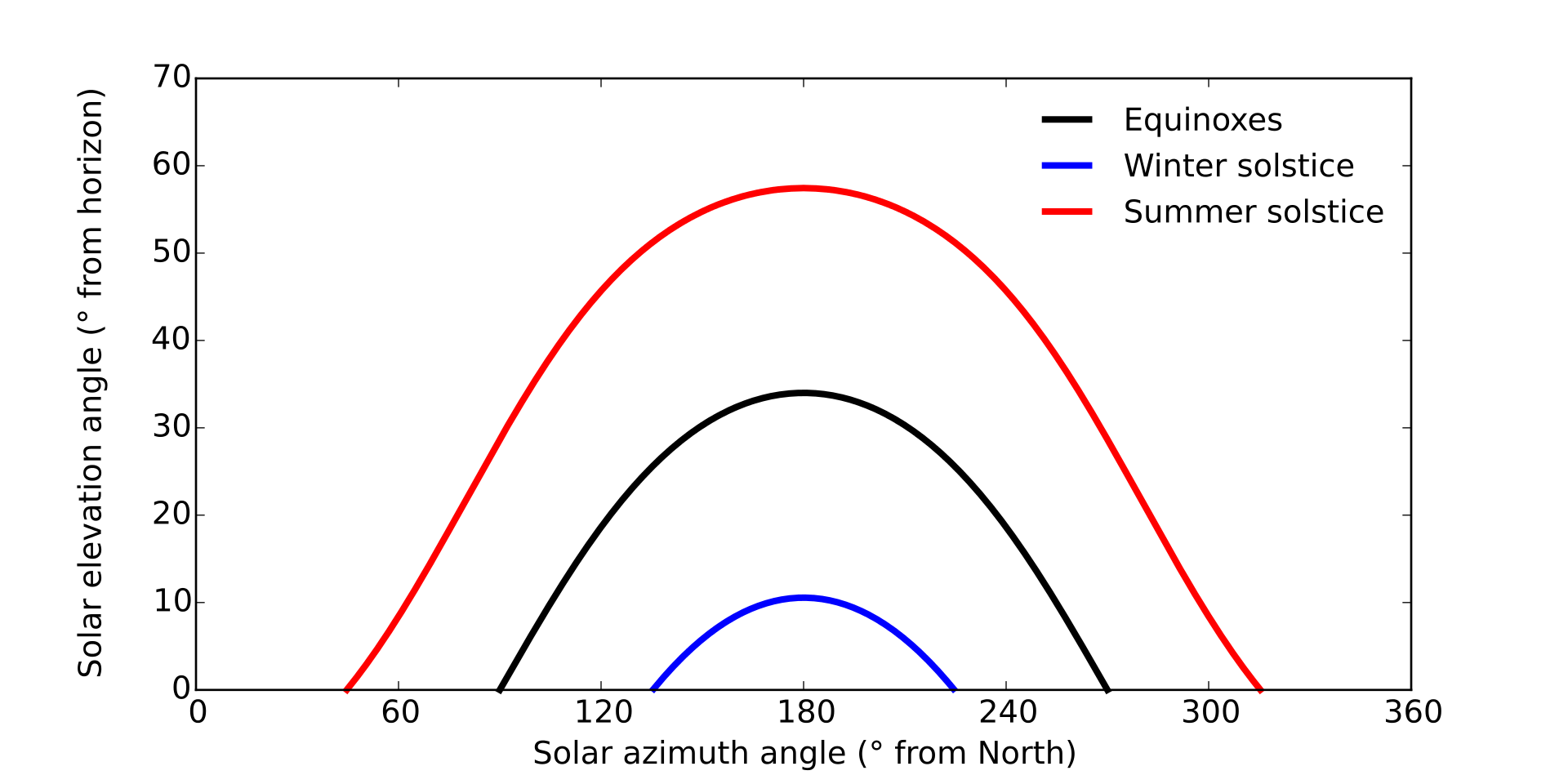
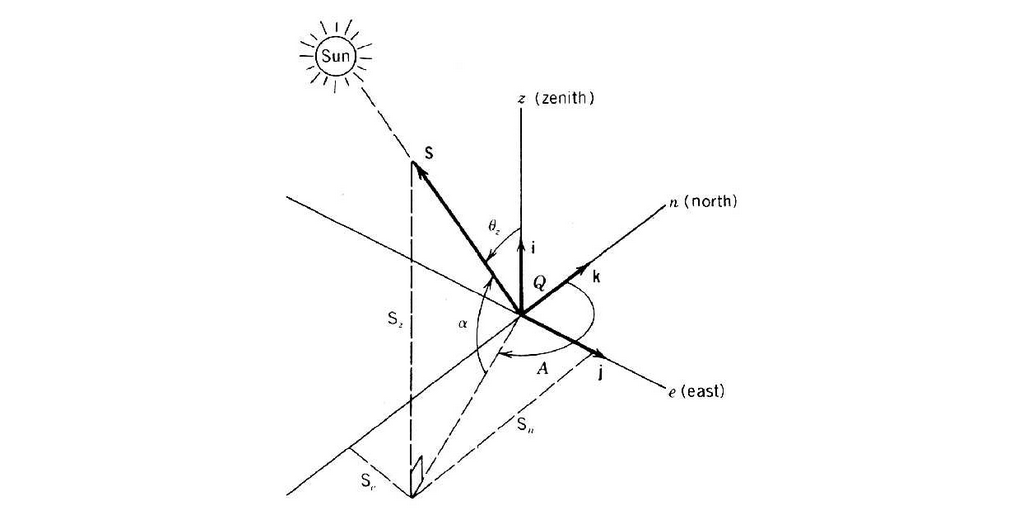
L’altitude du Soleil dépend de sa direction définie par la droite joignant les centres de la Terre et du soleil, ainsi que de la position de l’observateur à la surface terrestre et du temps. Voir Figure 4.12.
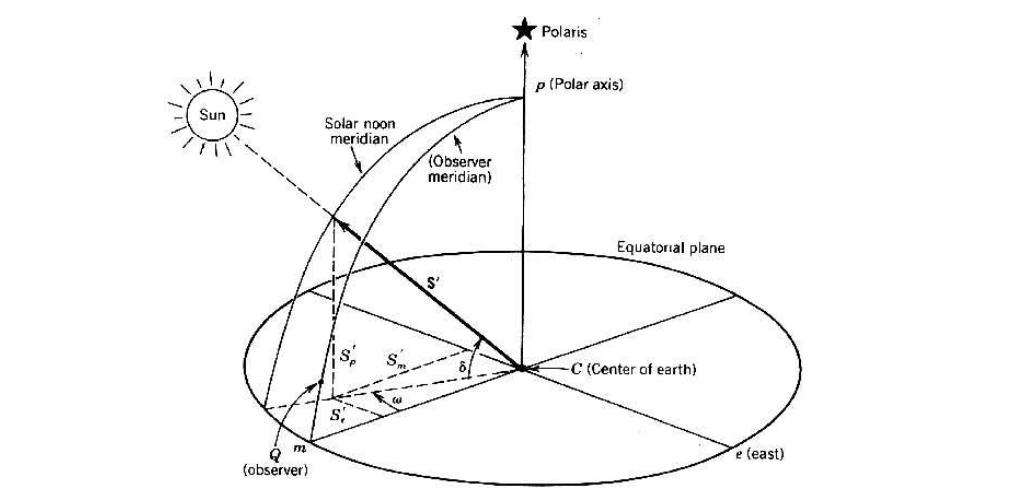
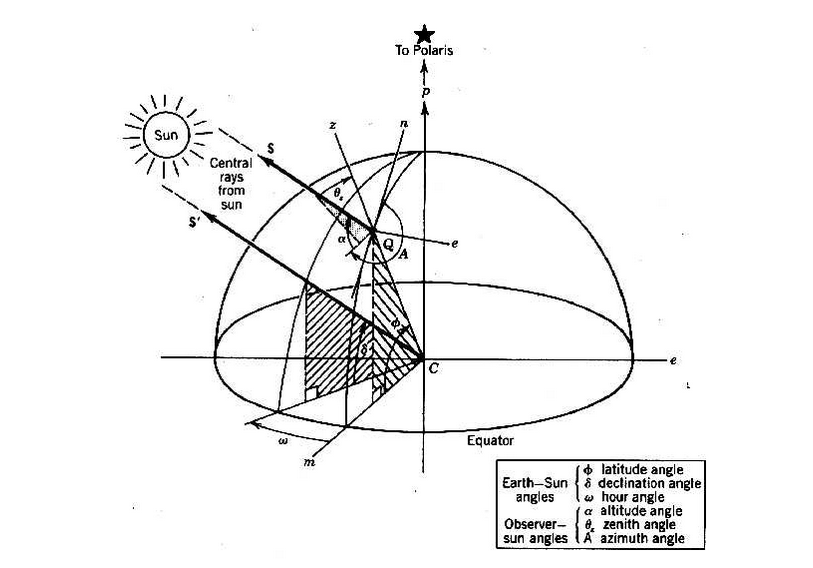
Après quelques manipulations mathématiques, on trouve que le sinus de l’altitude du soleil peut être calculé par l’Équation 4.20, et le rayonnement incident par l’Équation 4.21
Les symboles repris dans ces formules, sont décrits ci-après :
| L’altitude du Soleil en un point de la surface terrestre à un instant donné. | |
| La déclinaison du Soleil à un instant donné. | |
| La latitude du point d’observation sur la surface terrestre. | |
| L’angle horaire, qui est la différence entre la longitude du point d’observation et la longitude du méridien contenant le vecteur de la direction du Soleil à un instant donné. | |
| Le rayonnement incident par unité de surface en un point de la surface terrestre à un instant donné, pour un rayonnement unitaire au sommet de l’atmosphère. | |
| La distance Terre - Soleil à un instant donné. | |
| La distance Terre – Soleil moyenne = 1 unité astronomique | |
| La distance Terre – Soleil à un instant donné, exprimée en unité astronomique |
La déclinaison du soleil, la longitude du vecteur de sa direction et la distance Terre-Soleil dépendent du temps. Elles sont calculées en utilisant des tables d’éphémérides et des programmes publiés par le Jet Propulsion Laboratory. La matière est très touffue, et il n’est pas facile de trouver son chemin. Il existe heureusement des packages en langage Python (SpiceyPy et Skyfield qui facilitent quelque peu les calculs.
Le rayonnement solaire incident a été calculé pour chacun des 64800 points de la surface de la planète, toutes les 10 minutes pour une année complète, avec des moyennes par jour, par mois et pour l’année entière.
Quelques résultats de calcul sont repris à la Figure 4.14.
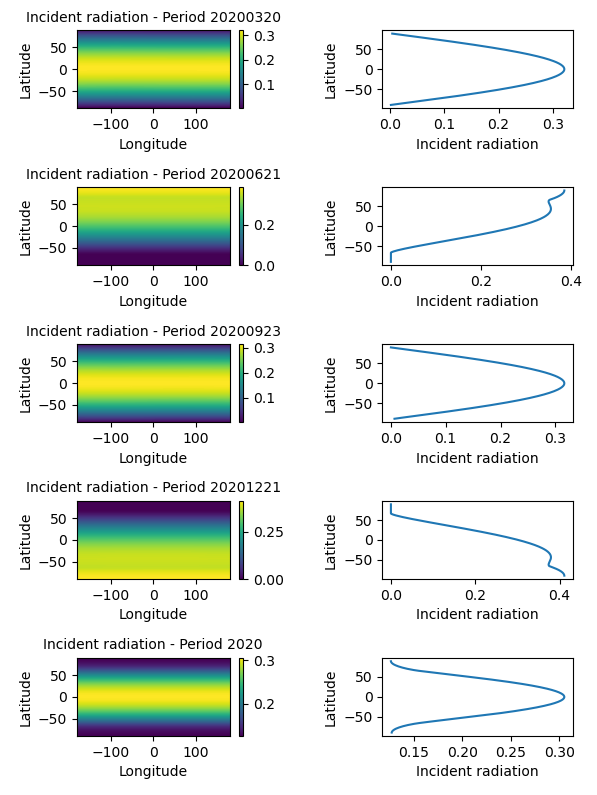
4.6.4 Comparaison des températures hadisst et du rayonnement solaire incident
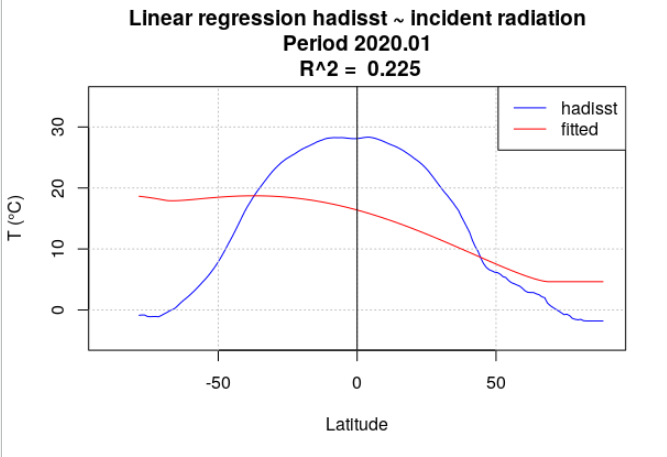
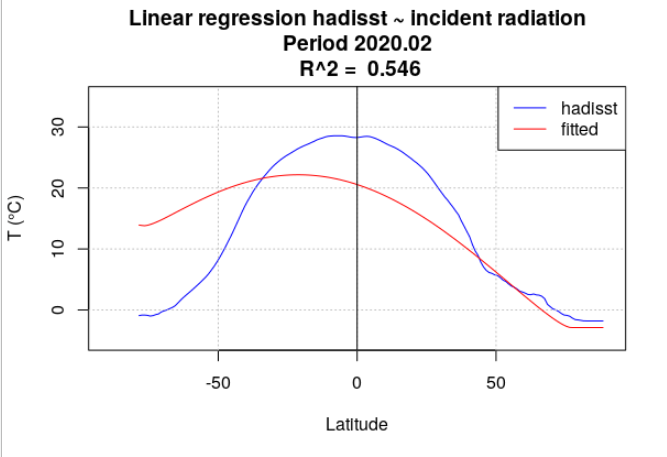
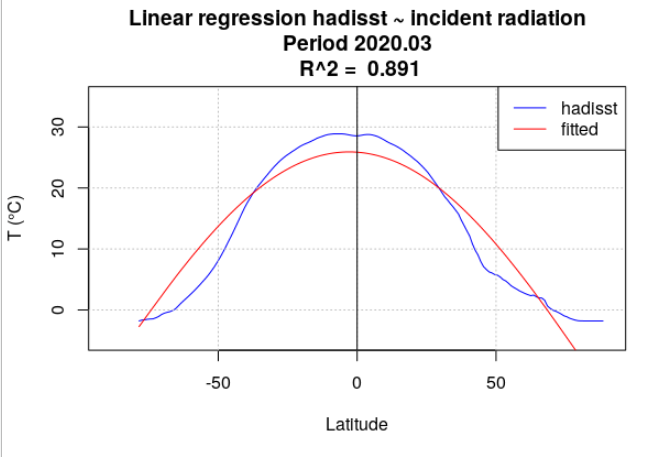
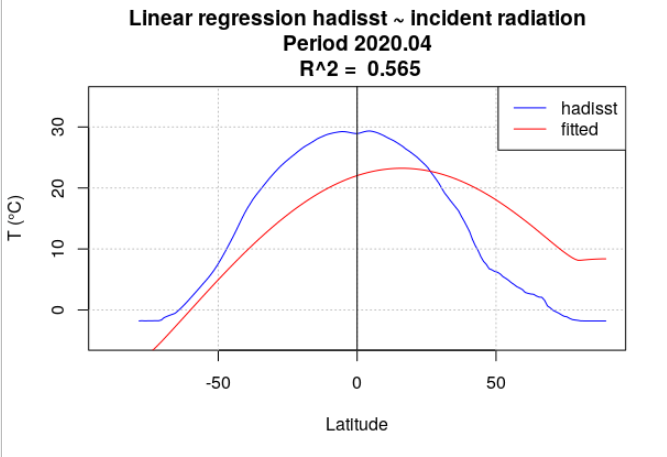
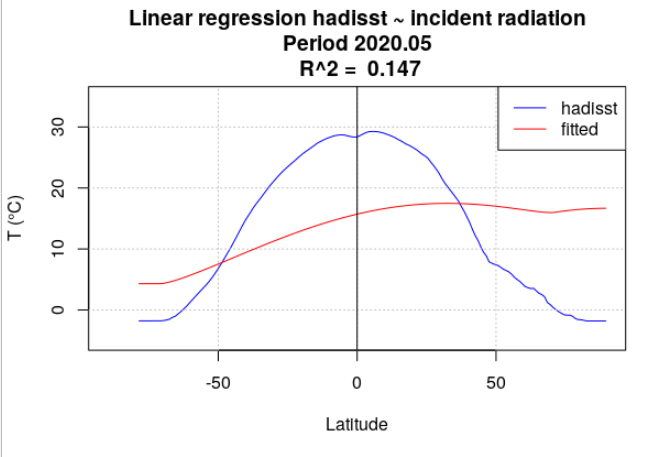
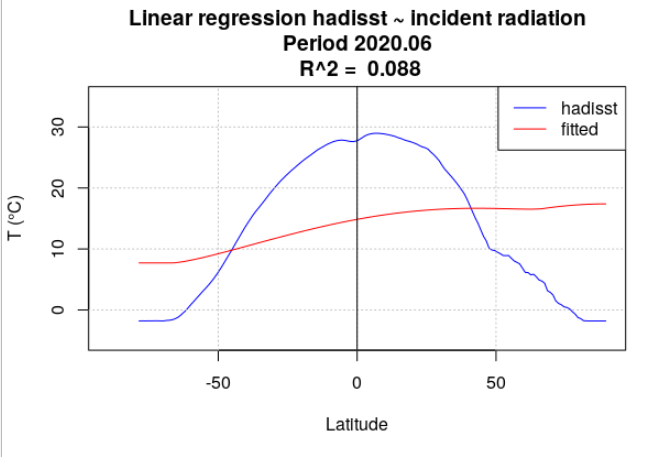
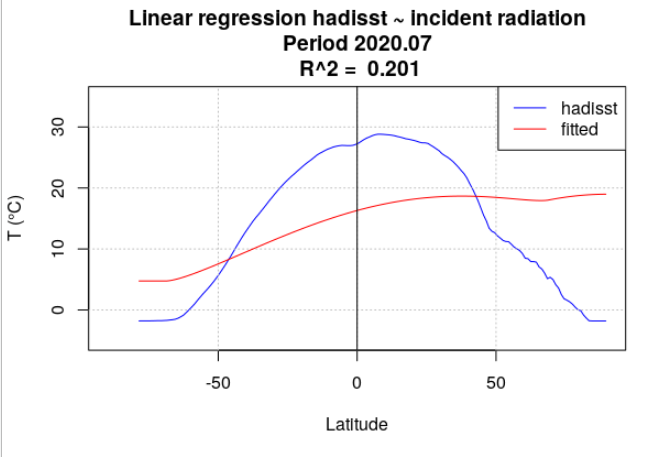
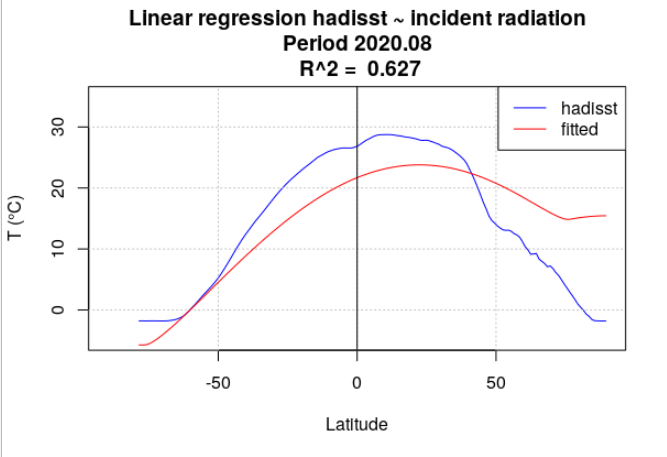
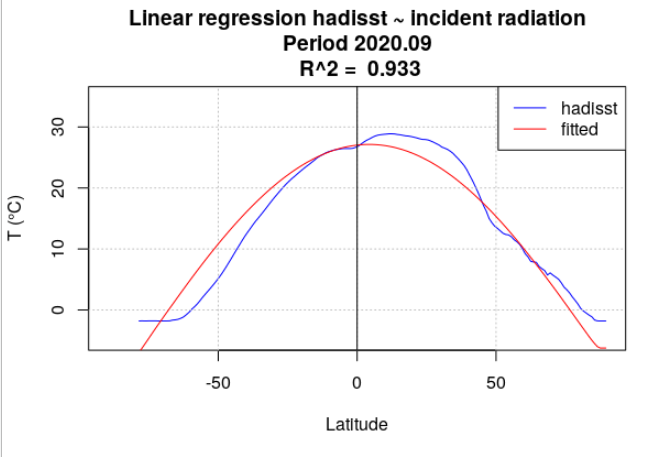
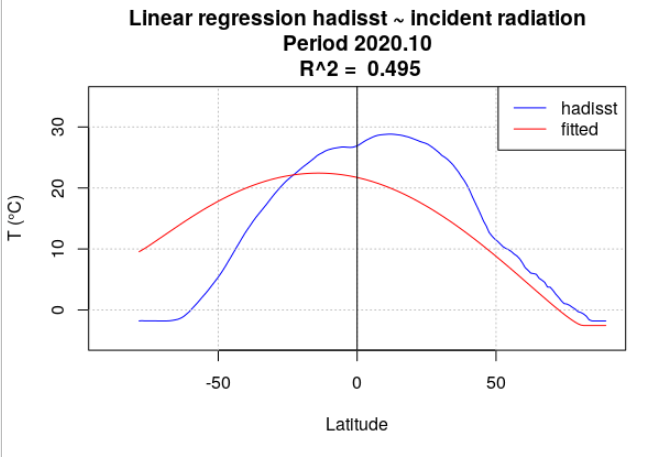
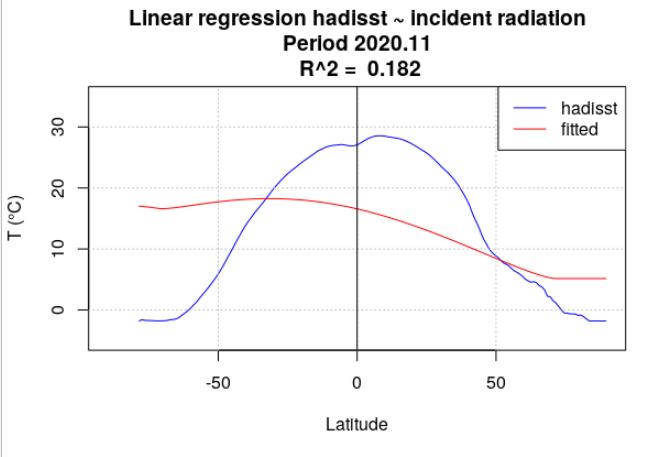
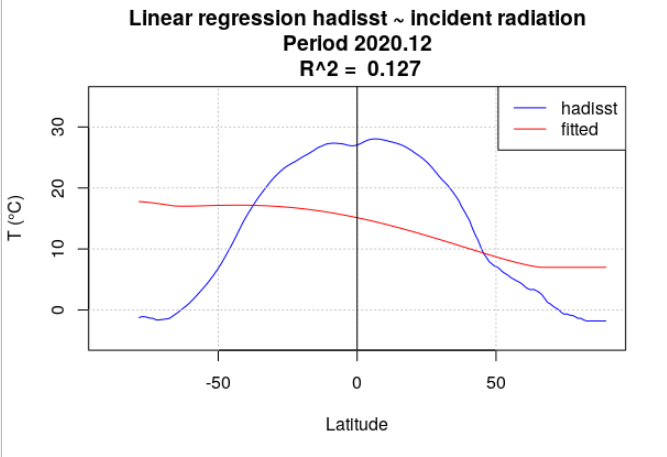
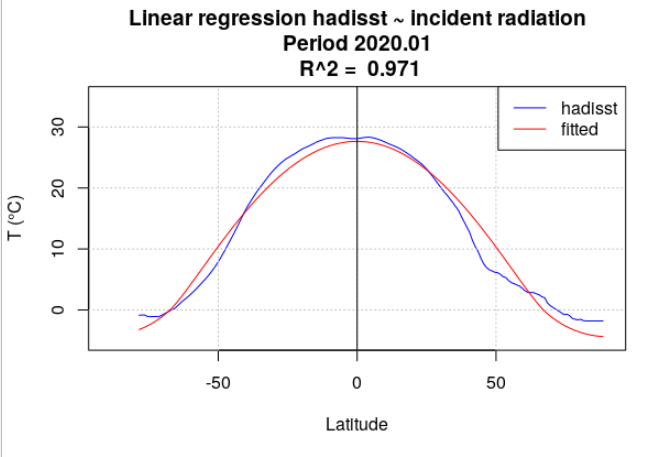
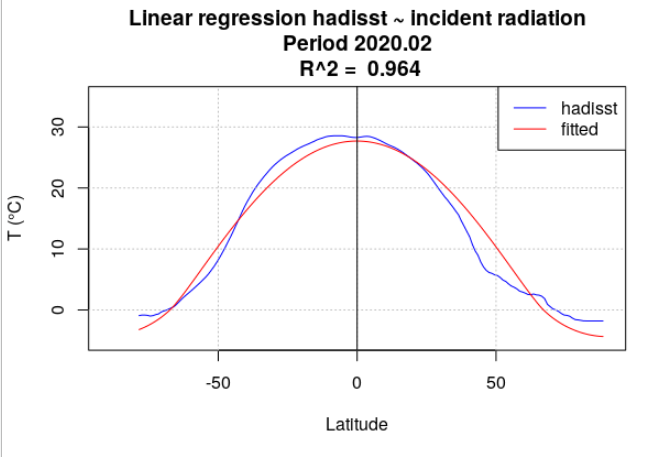
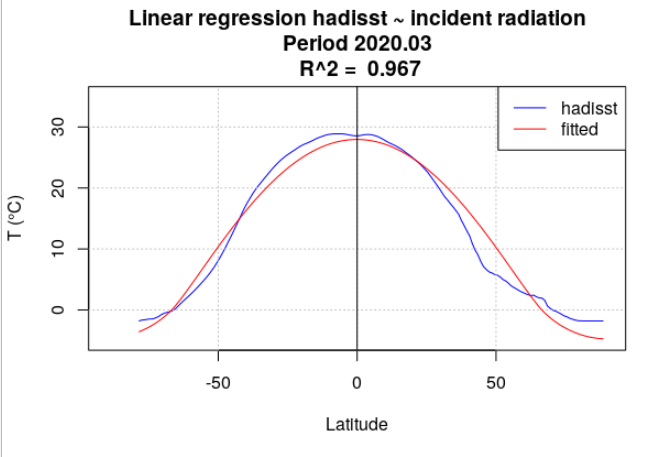
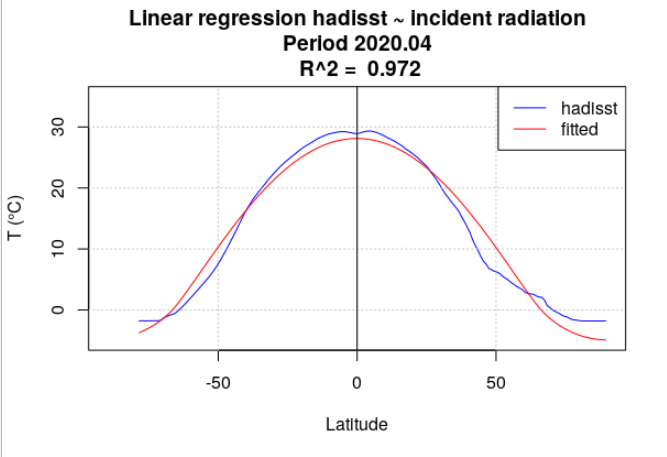
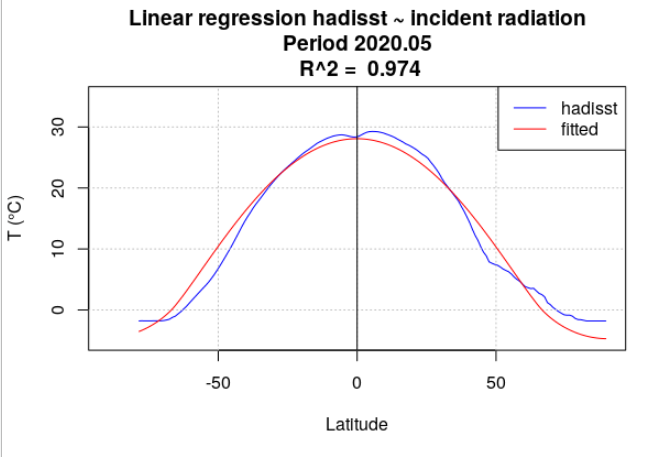
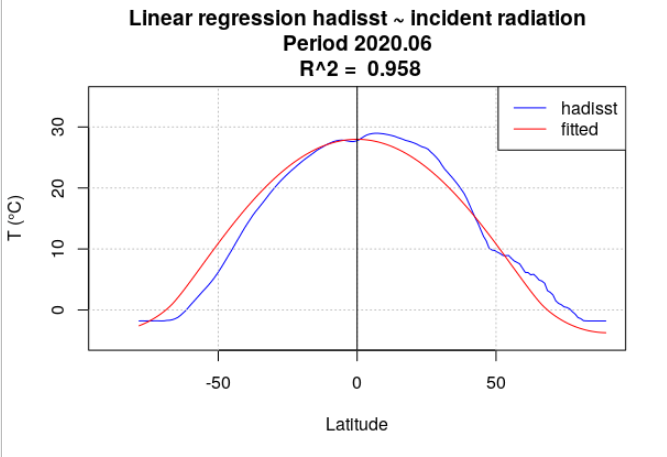
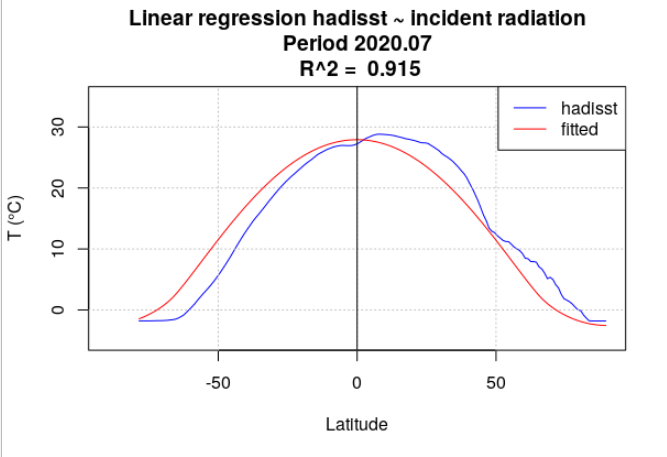
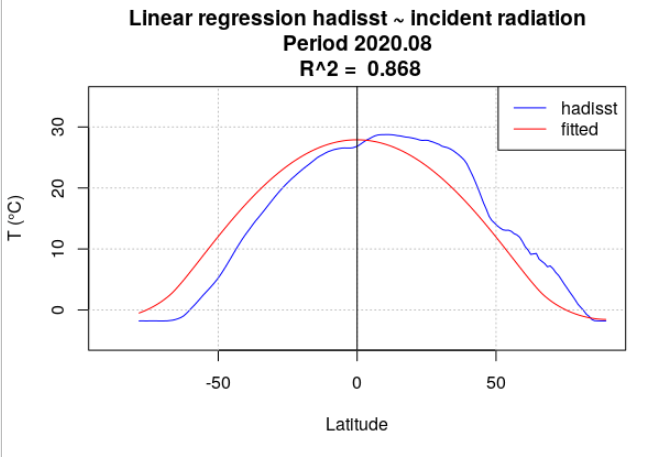
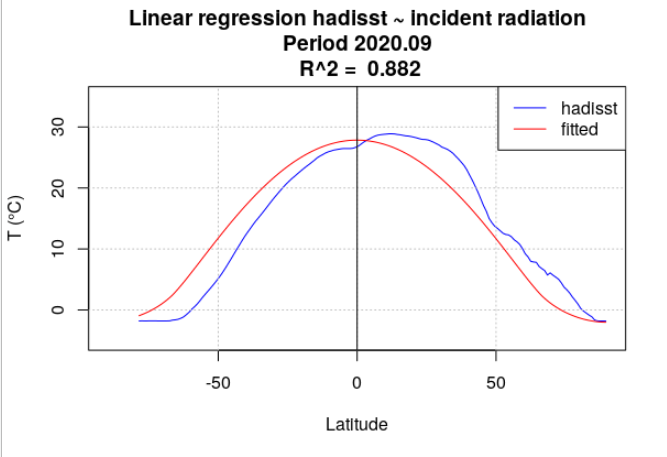
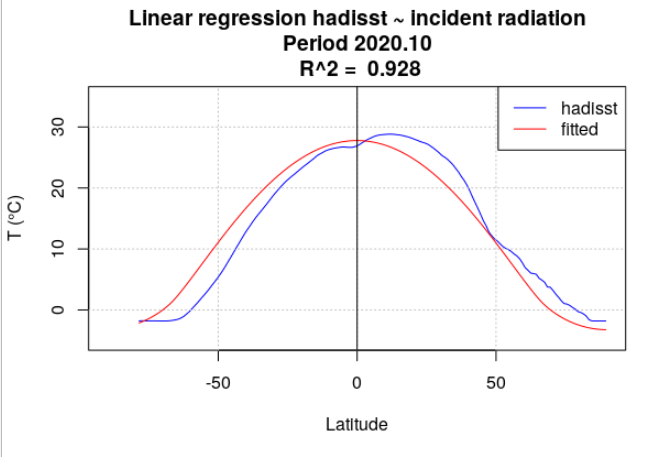
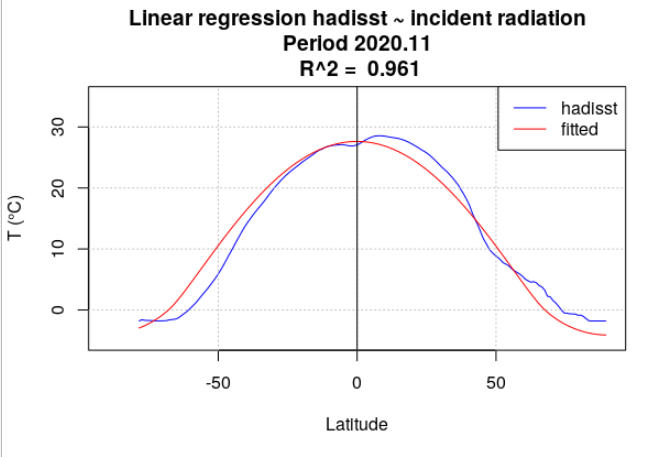
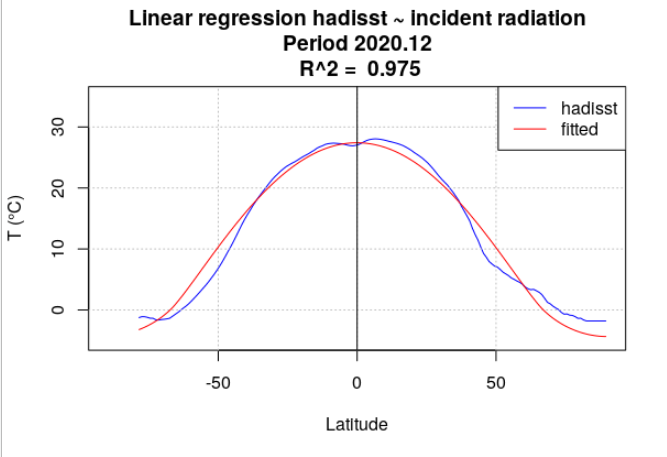
Pour tous les mois de l’année 2020, la température de surface océanique hadisst a été moyennée par latitude. Le rayonnement incident a également été moyenné par latitude, en se limitant aux points considérés comme « océan » dans la série hadisst. Une analyse de régression a chaque fois été menée entre la température hadisst et le rayonnement incident. Deux séries de calculs ont été effectuées. Dans la première série, le rayonnement incident moyen du mois a été utilisé (Figure 4.15). Dans la seconde série, le rayonnement incident moyen de l’année a été utilisé (Figure 4.16).
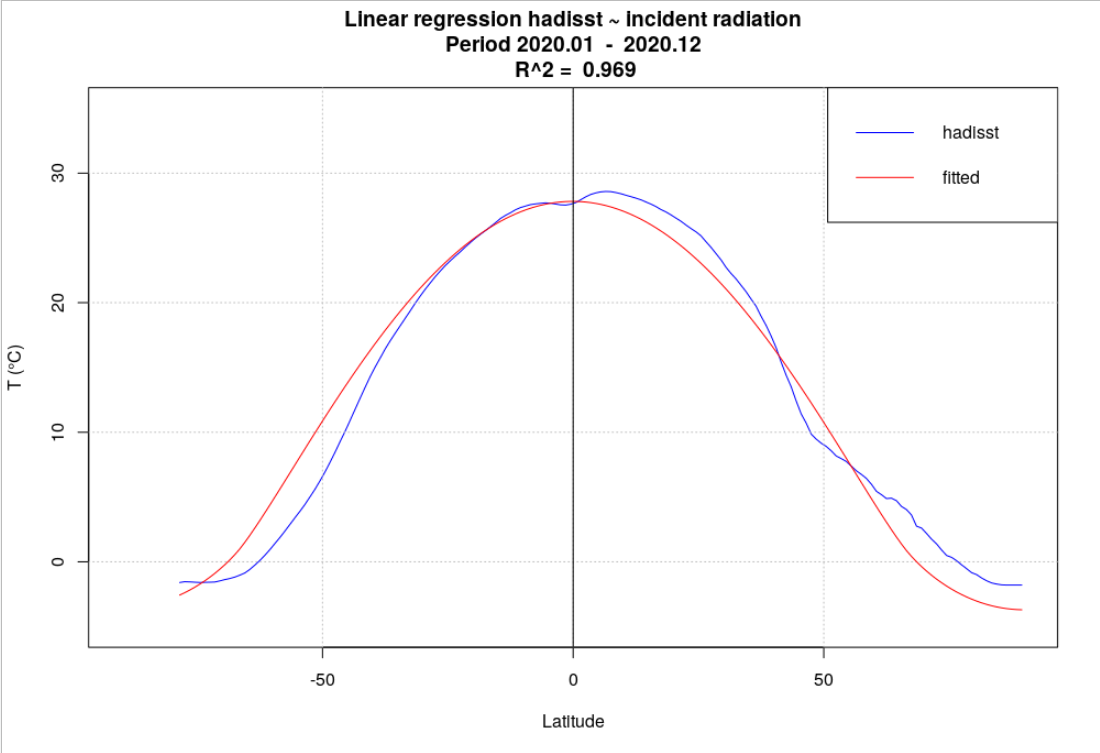
Finalement, la régression de la température océanique moyenne annuelle par latitude de hadisst par le rayonnement incident moyen annuel a également été calculée (Figure 4.17). La corrélation est quasiment parfaite, et permet de conclure que les observations montrent que la répartition de la température océanique découle de celle du rayonnement incident annuel. Ceci a d’importantes conséquences quant à l’usage de moyennes spatiales et temporelles des températures océaniques dans les études climatiques. Ceci est discuté dans la section suivante.
4.6.5 Réhabilitation des anomalies de température
L’examen de la série de température hadisst révèle qu’à une latitude donnée, les températures de surface océaniques varient peu à latitude constante, et qu’en moyenne annuelle, en formalisant l’analyse de régression ( Figure 4.17), on a :
Dans cette formule,
| = la latitude. | |
| = la température annuelle locale moyenne à la latitude considérée. | |
| = une température de référence. | |
| = une constante. | |
| = le rayonnement incident annuel moyen à la latitude considérée, pour une irradiance totale solaire unitaire au sommet de l’atmosphère. |
En intégrant cette expression sur la surface des océans, et en divisant par la surface totale océanique, on obtient une anomalie globale moyenne :
En considérant une Terre sphérique de rayon R, l’élément de surface dS en coordonnées sphériques est égal à :
Pour calculer la moyenne d’une grandeur sur une sphère, il faut la pondérer par le cosinus de sa latitude.
L’Équation 4.23 peut s’écrire
Dans cette formule,
| = l’anomalie globale de température annuelle moyenne pour une température de référence |
|
| = la température globale annuelle moyenne | |
| = le rayonnement global incident annuel moyen. Ce terme ne dépend que de la géométrie de la planète et de son orbite autour du Soleil. |
Moyennant un choix adéquat de sa température de référence, l’anomalie globale de température annuelle moyenne est proportionnelle au rayonnement incident annuel moyen.
Bien que la température de surface océanique soit une grandeur intensive, il est tout à fait légitime d’en faire des moyennes spatiales pour calculer une anomalie globale, parce qu’en procédant ainsi, on ne fait que moyenner des rayonnements, ce qui est tout à fait correct. C’est l’Équation 4.22 qui justifie cette pratique.
L’Équation 4.25 s’adapte facilement si une anomalie de température utilise une autre température de référence
Dans cette relation,
Pour passer du rayonnement unitaire au rayonnement au sommet de l’atmosphère, il suffira de modifier la constante de proportionnalité . On aura alors
Dans cette formule,
| = une constante | |
| = le rayonnement annuel au sommet de l’atmosphère | |
| = un rayonnement au sommet de l’atmosphère de référence |
l’Équation 4.27 est valable lorsque le rayonnement solaire au sommet de l’atmosphère est constant. Remarquons que dans ce cas,
L’Équation 4.27 se transforme alors en
On retrouve ainsi la solution approchée de l’équation différentielle du modèle thermique simple (Équation 4.13), telle que décrite à la Section 4.3. Cette solution est valable lorsque le rayonnement solaire au sommet de l’atmosphère n’est pas constant, à condition de faire un choix approprié de
4.6.6 Synthèse
A chaque latitude, et à chaque instant, les moyennes annuelles des températures de surface océaniques sont très bien modélisées par le rayonnement solaire incident.
Il est tout à fait légitime d’effectuer des moyennes spatiales et temporelles des températures de surface océaniques.
Travailler avec des températures ou avec leurs anomalies est équivalent, à une translation près.
Lorsqu’on détermine une tendance temporelle, on risque d’introduire un biais si la durée de la période utilisée pour déterminer la tendance n’est pas sensiblement plus longue que la durée du cycle, mais le biais sera le même avec la température ou avec son anomalie.
Indépendamment de ce qui précède, il serait préférable de travailler avec la température plutôt qu’avec son anomalie, parce que dans ce dernier cas, on perd de l’information :
La variabilité saisonnière annuelle disparaît.
La variabilité spatiale disparaît également. Sur base des anomalies de température, il est impossible de voir que le rayonnement incident est responsable de la distribution de la température par latitude.
4.7 Analyses effectuées au moyen du modèle dynamique
4.7.1 Sélection des variables indépendantes dans les analyses de régression TS (température - soleil)
Les matrices de corrélation de la Section 2.6.1.1 montrent que l’activité solaire moyennée nrl2TsiAvg est meilleure que la série histTsiAvg et que la série sunspots. Les tests de causalité de la Section 2.6.2.2 montrent une causalité bidirectionnelle entre la température de surface océanique (hadsst3) et le logCO2, ainsi qu’une causalité unidirectionnelle de l’activité solaire moyennée vers hadsst3. Un terme harmonique (harm), comme dans l’Équation 4.3 a également été pris en compte.
Toutes les combinaisons possibles des variables indépendantes harm, nrl2TsiAvg, et logCO2 ont été utilisées pour modéliser la variable dépendante hadsst3 par analyse de régression.
Les résultats de ces analyses sont résumées dans la Table 4.2.
| harm | nrl2TsiAvg | logCo2 | CV | AIC | AICc | BIC | AdjR2 | %SE harm | %SE nrl2TsiAvg | %SE logCo2 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | x | 0.0157 | -8452.2 | -8452.1 | -8452.2 | 0.793 | 4.05 | 1.24 | ||
| x | x | x | 0.0157 | -8450.8 | -8450.8 | -8450.8 | 0.793 | 4.04 | 5.16 | 80.15 |
| x | x | 0.0165 | -8346.5 | -8346.4 | -8346.5 | 0.782 | 3.62 | 1.17 | ||
| x | 0.0183 | -8131.8 | -8131.8 | -8131.8 | 0.758 | 1.25 | ||||
| x | x | 0.0184 | -8129.8 | -8129.8 | -8129.8 | 0.758 | 4.56 | 665.40 | ||
| x | 0.0227 | -7700.0 | -7700.0 | -7700.0 | 0.701 | 1.45 | ||||
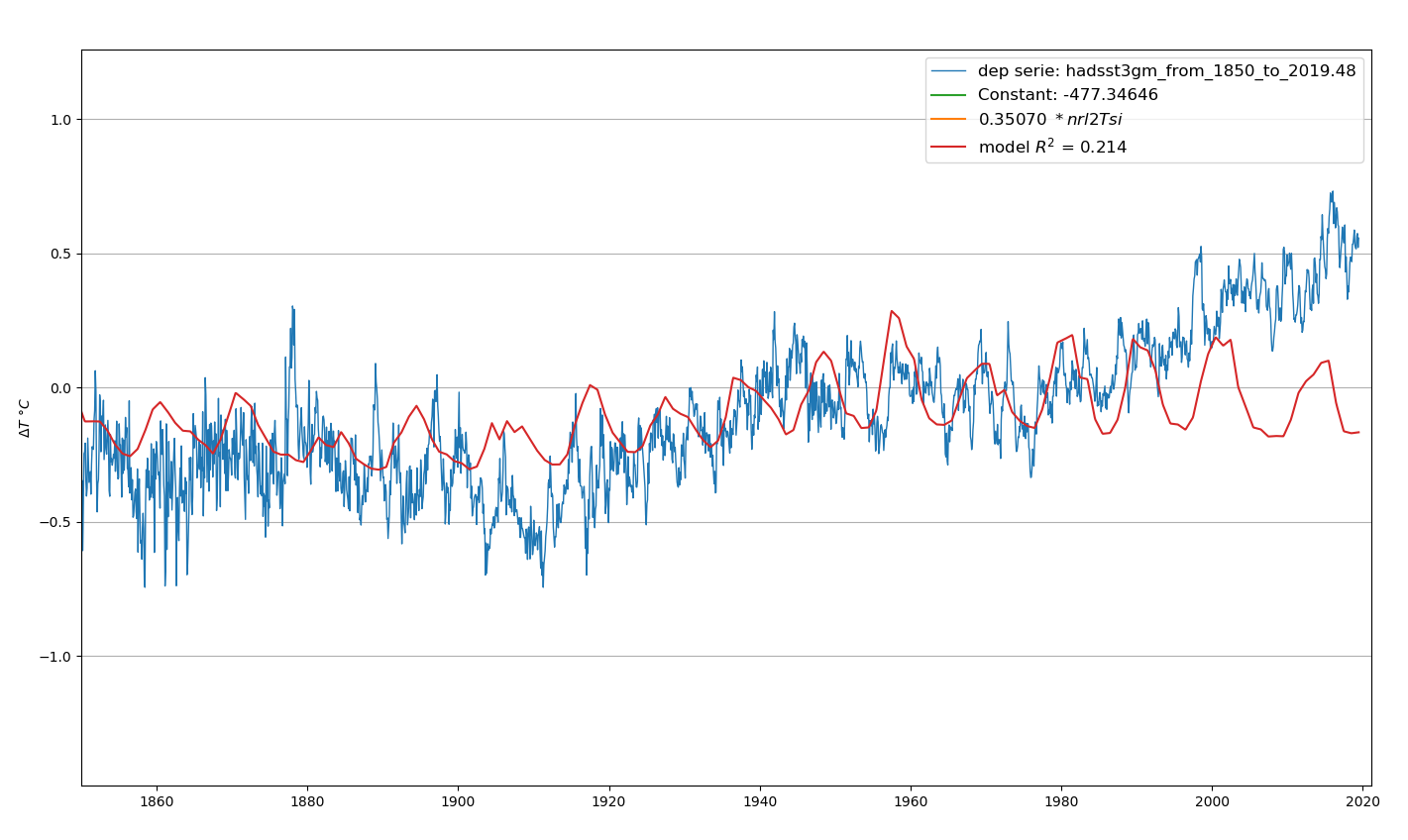
| x | 0.0627 | -5631.2 | -5631.2 | -5631.2 | 0.173 | 4.85 |
La table est triée par capacité prédictive décroissante. Les trois dernières colonnes reprennent le pourcentage de l’erreur standard sur le coefficient de chaque terme de régression utilisé. La meilleure solution est donnée par la combinaison d’un terme harmonique et de l’ITS moyenne.
L’ajout d’un terme log(CO2) détériore la situation. Seul, ou en combinaison avec un terme harmonique, le log(CO2) donne un résultat correct, mais moins bon. Lorsqu’il est combiné avec l’ITS moyenne, l’erreur sur son coefficient devient très importante, alors que les erreurs sur les coefficients du terme harmonique et de l’ITS moyenne sont peu affectées.
De plus nous avons montré à la Section 2.6.3.3 que l’évolution du CO2 suit celle de la température avec un décalage de 8 mois.
On peut en conclure que rien ne justifie l’introduction d’un terme log(CO2) dans les analyses de régression TS.
Nous verrons plus tard au Chapitre 6, qu’en dehors des émissions anthropiques, le CO2 naturel dépend de la température suivant l’équilibre de Henry – van ’t Hoff. Suivant la même relation d’équilibre, le CO2 anthropique a un petit effet sur la température, mais il est suffisamment faible pour qu’on puisse le négliger dans les analyses.
Plusieurs analyses sont détaillées ci-après.
Les analyses TS.1, TS.2 et TS.3, basées uniquement sur l’activité solaire moyenne, n’ont été reprises que pour montrer de manière détaillée que des 3 variables sunspotsAvg, histTsiAvg et nrl2TsiAvg, c’est effectivement cette dernière qui est la meilleure, ce qui confirme ce qui a été trouvé à la Section 2.6.1.2.
4.7.2 Analyse TS.1: taches solaires et température
Cette analyse utilise les taches solaires (sunspots) comme mesure du rayonnement solaire. Voir Figure 4.18 et Figure 4.19
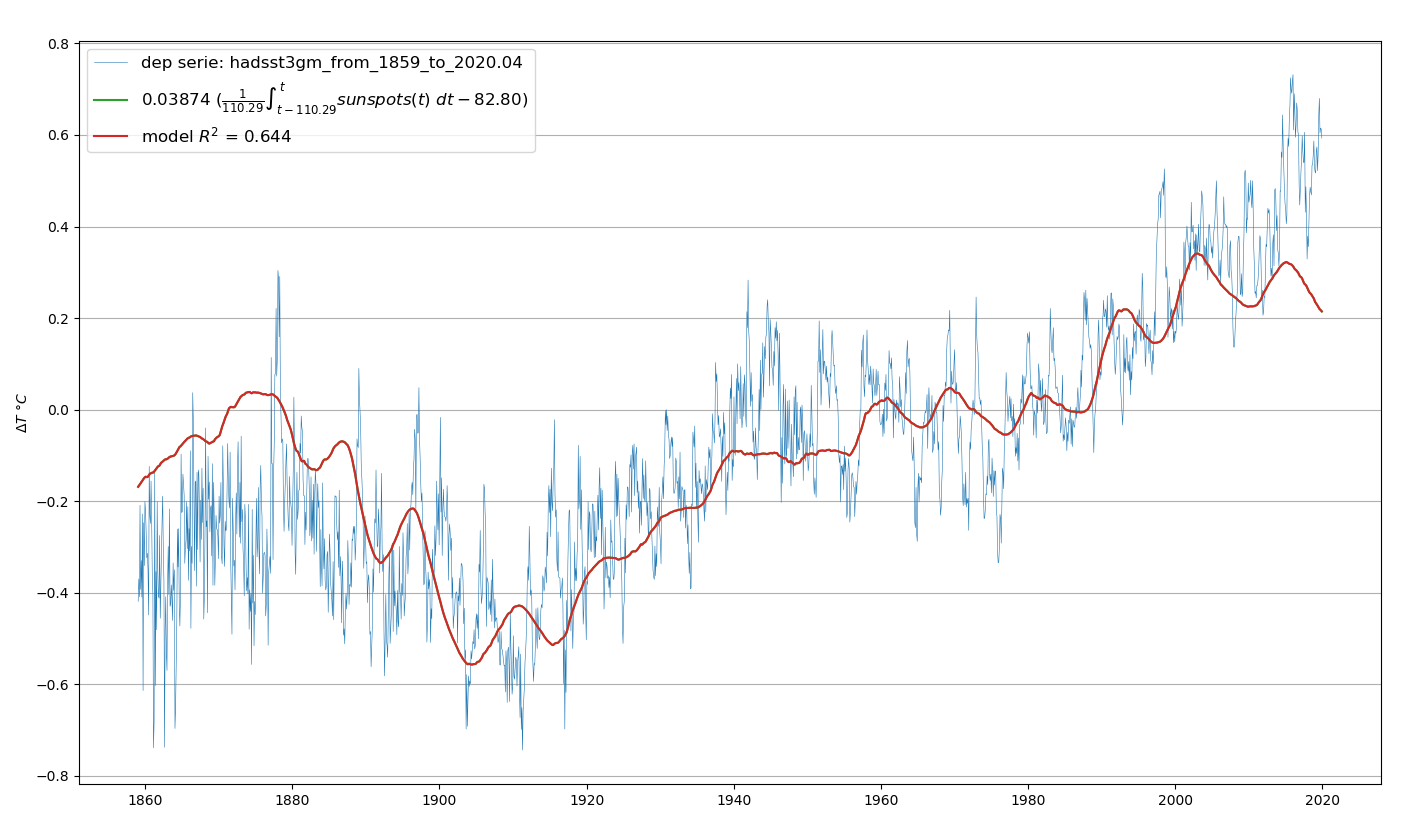
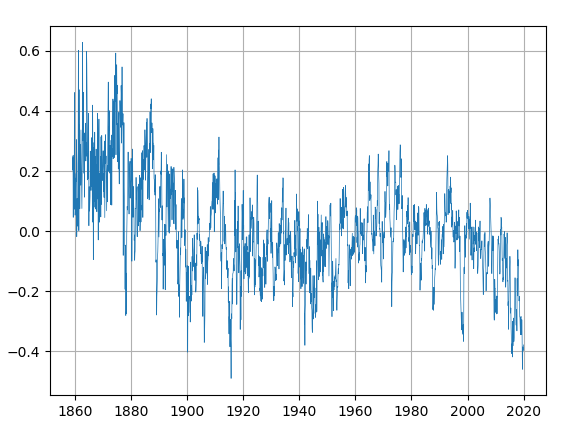
4.7.3 Analyse TS.2: irradiance totale solaire et température
Cette analyse utilise la reconstruction historical_tsi comme mesure du rayonnement solaire. Voir Figure 4.20 et Figure 4.21
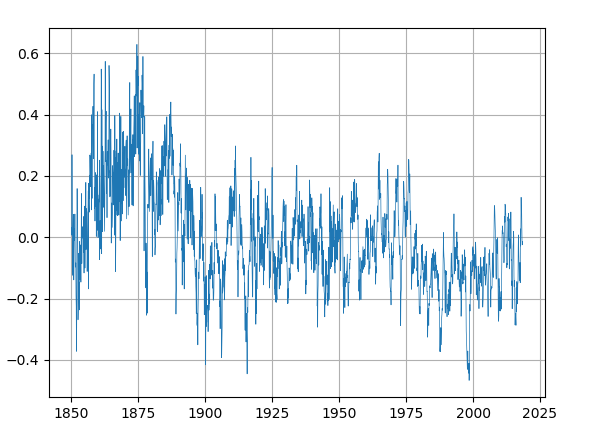
4.7.4 Analyse TS.3: irradiance totale solaire et température
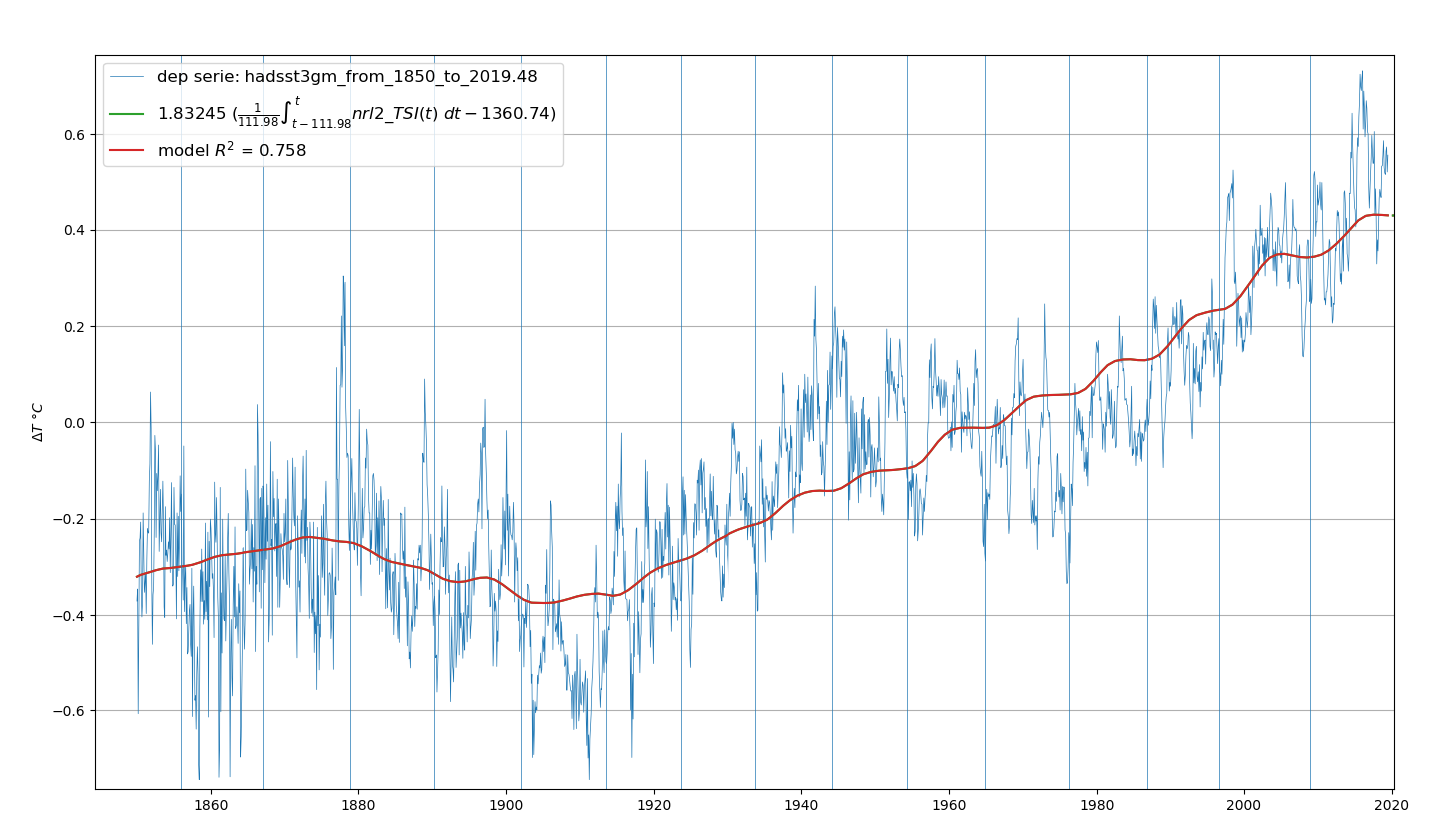
Cette analyse utilise la reconstruction nrl2_tsi comme mesure du rayonnement solaire. Voir Figure 4.22 et Figure 4.23.
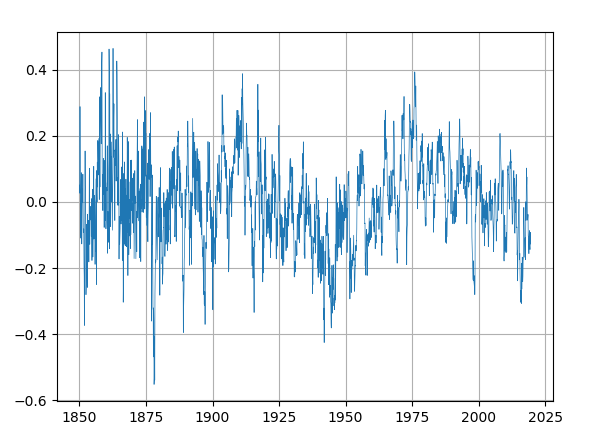
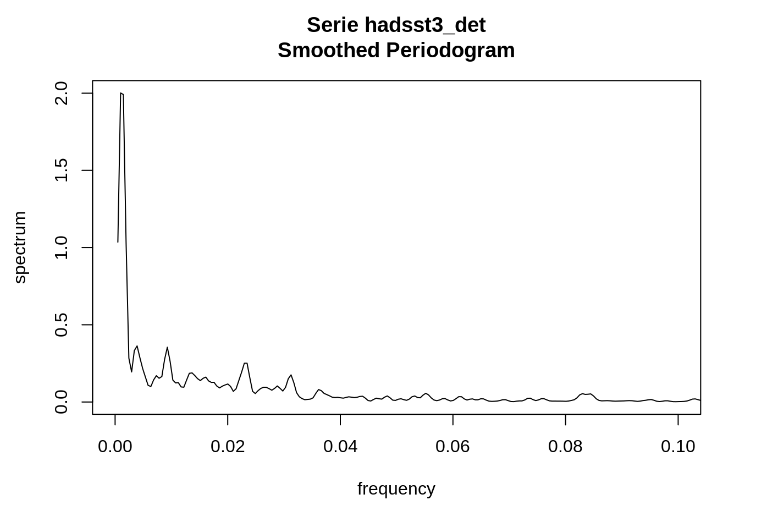
L’analyse spectrale de la série hadsst3gm après detrending cubique confirme la présence d’un pic important et de quelques pics secondaires de moindre amplitude. Voir Figure 4.24
Les périodes des 4 premiers pics principaux sont égales à 66,7 ans, 21,4 ans, 9,0 ans et 3,6 ans. La figure 4 dans l’article de (Scafetta 2021) contient des pics très voisins.
Sur cette base, un terme harmonique a été ajouté dans l’analyse suivante conformément à l’Équation 4.3.
4.7.5 Analyse TS.4: TS.3 + un terme harmonique
Cette analyse utilise la reconstruction nrl2_tsi et un terme harmonique dont la période calculée par analyse de régression multiple non linéaire vaut 66.28 ans. Cette valeur est très voisine de la période de 66.7 ans trouvée dans l’analyse spectrale précédente. Voir Figure 4.25 et Figure 4.26
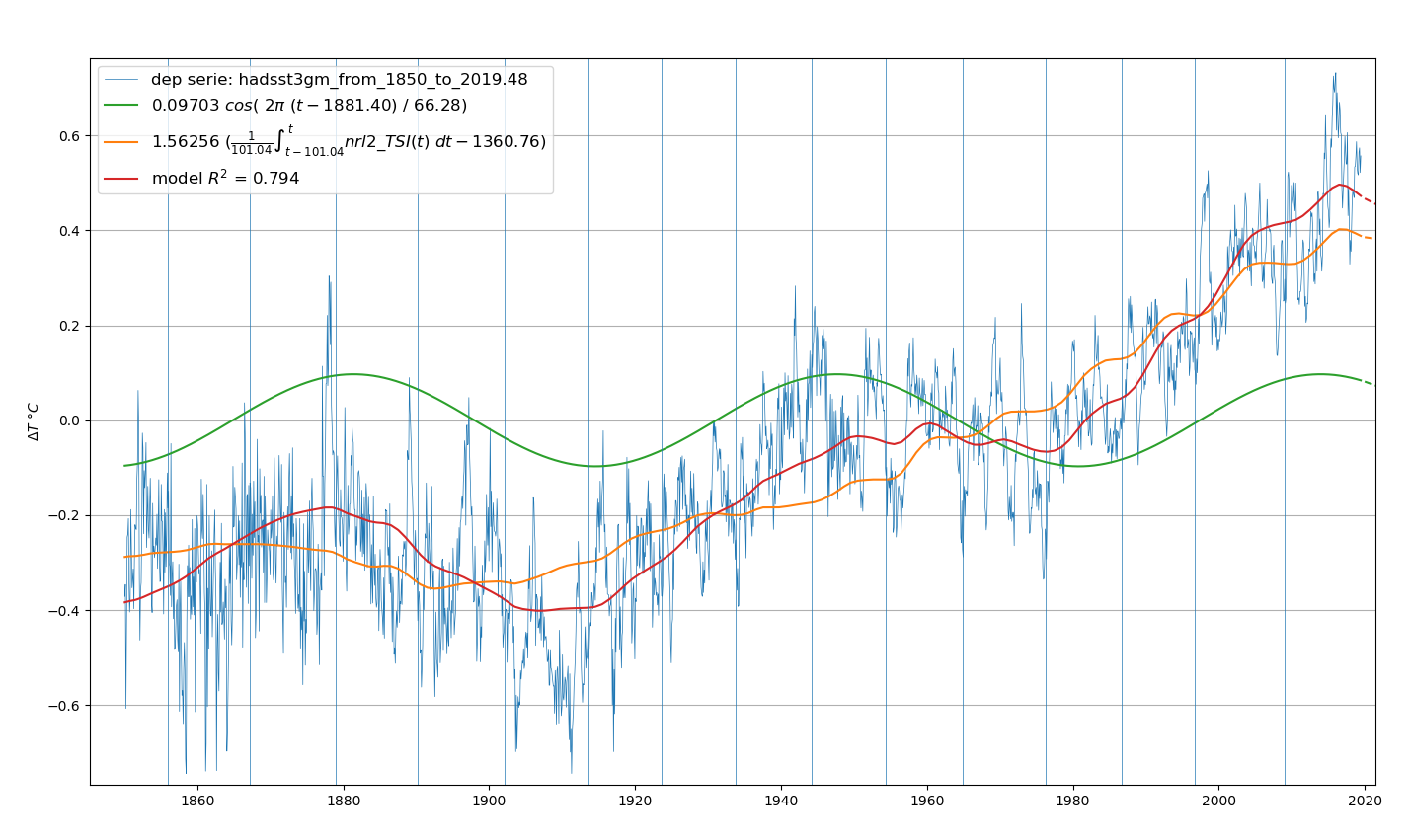
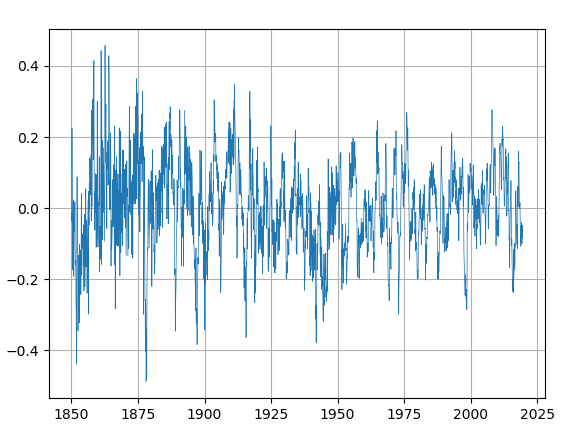
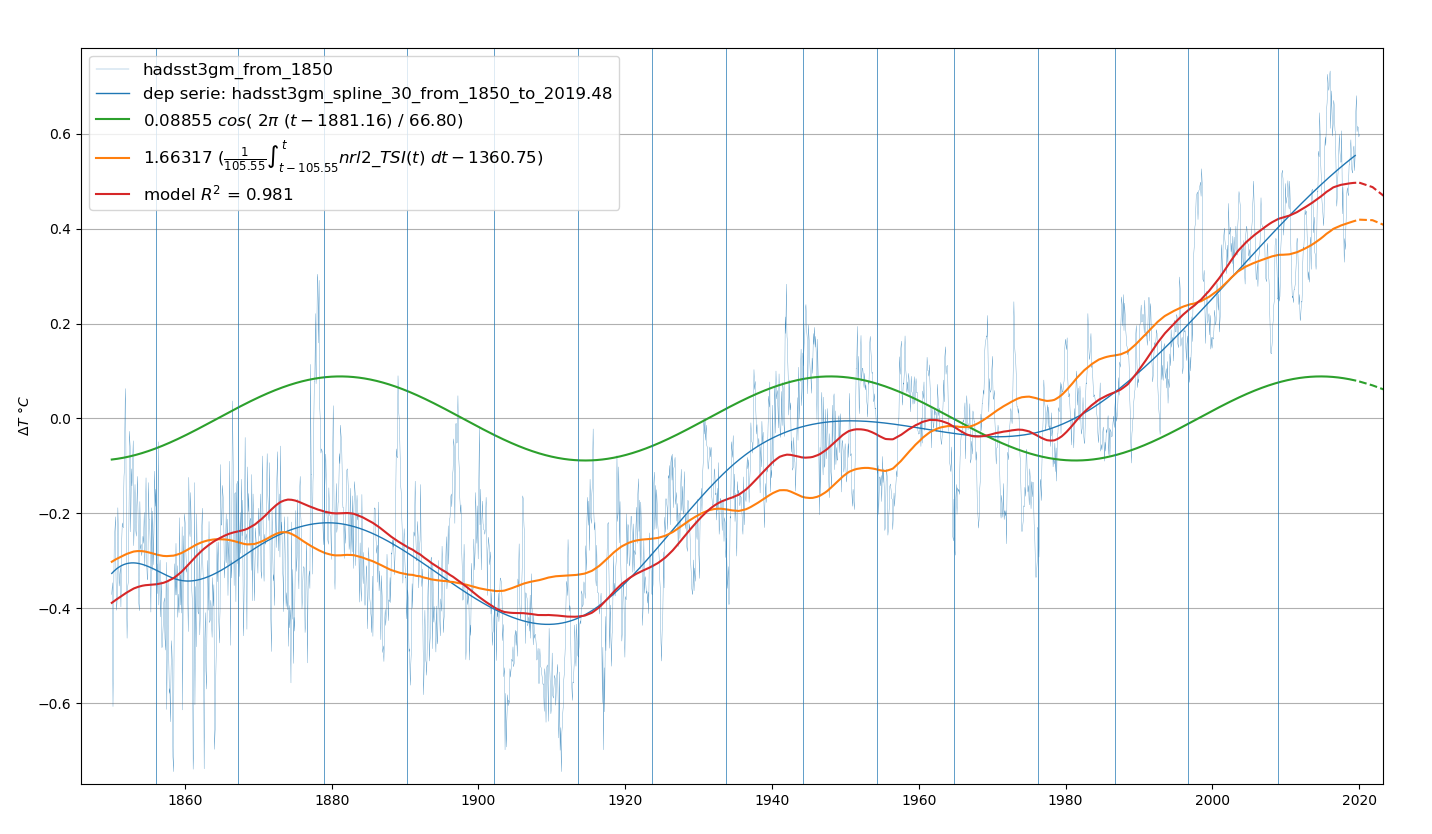
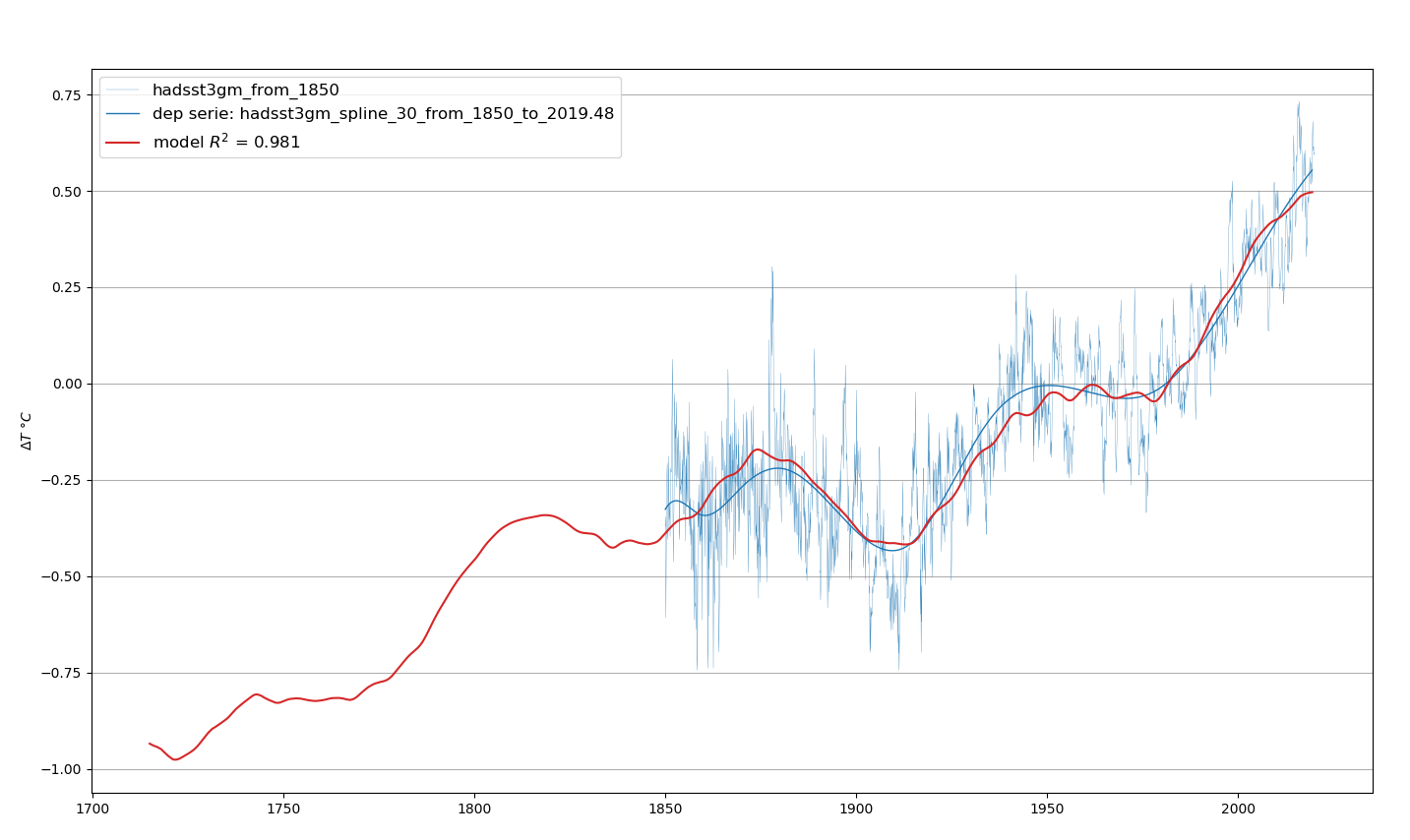
4.7.6 Analyse TS.5: TS.4 + lissage de la température
C’est la même analyse que l’analyse TS.4, sauf que le relevé des températures a fait l’objet d’un lissage par spline de degré 3 pour éliminer les épisodes El Niño/La Niña et l’impact des éruptions volcaniques. Ces éléments qui « perturbent » l’analyse n’ont pas d’influence sur le climat parce qu’ils sont plus ou moins cycliques ou ont une brève durée. Le lissage affecte peu les paramètres du modèle, mais révèle la véritable corrélation.
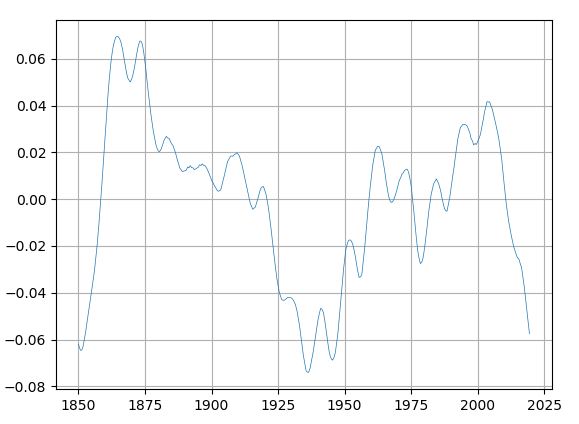
4.7.7 Analyse TS.6: une projection rétrospective
C’est la même analyse que l’analyse TS.4, mais en se plaçant rétrospectivement en l’an 2000. Cette analyse a été menée afin d’évaluer les capacités prédictives du modèle et de voir comment l’anomalie de température évolue dans le futur. Les mesures antérieures à 2000 servent à calibrer le modèle, tandis que les mesures plus récentes servent à le valider.
Il est difficile d’utiliser le modèle pour faire des prévisions parce qu’il est basé sur l’irradiance totale solaire qui est encore plus difficile à prédire que les taches solaires.
L’option choisie considère que le rayonnement solaire futur est constant et égal à la valeur du rayonnement solaire moyen en 2000 (modèle prédictif simple dit “naïf”), soit 1360.9 W/m2 (Voir Figure 4.29). Cette hypothèse est en dessous de la réalité puisque le rayonnement solaire moyen a continué à augmenter après l’an 2000, avant de commencer à décroître légèrement (Cfr Figure 2.5 ).
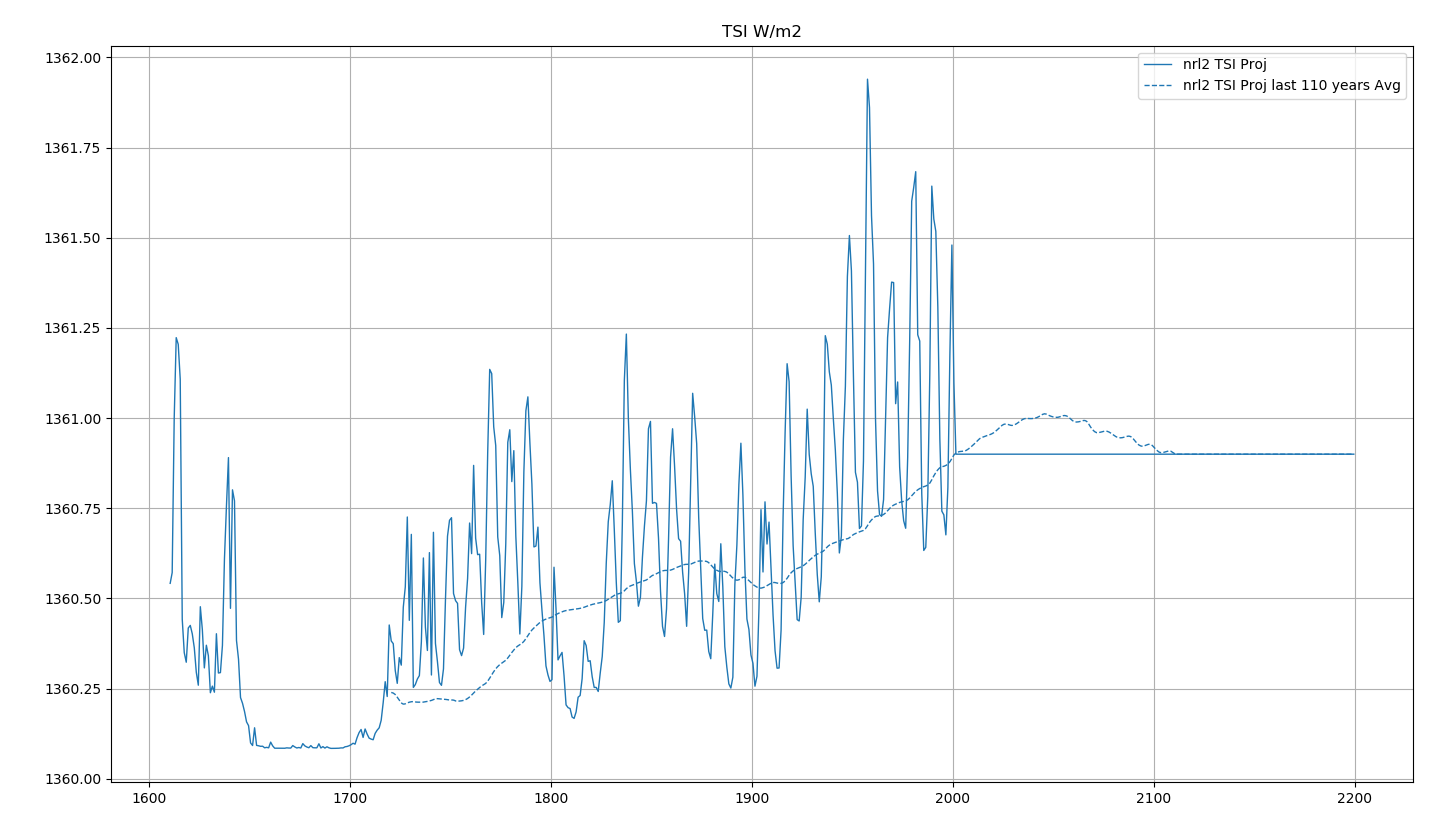
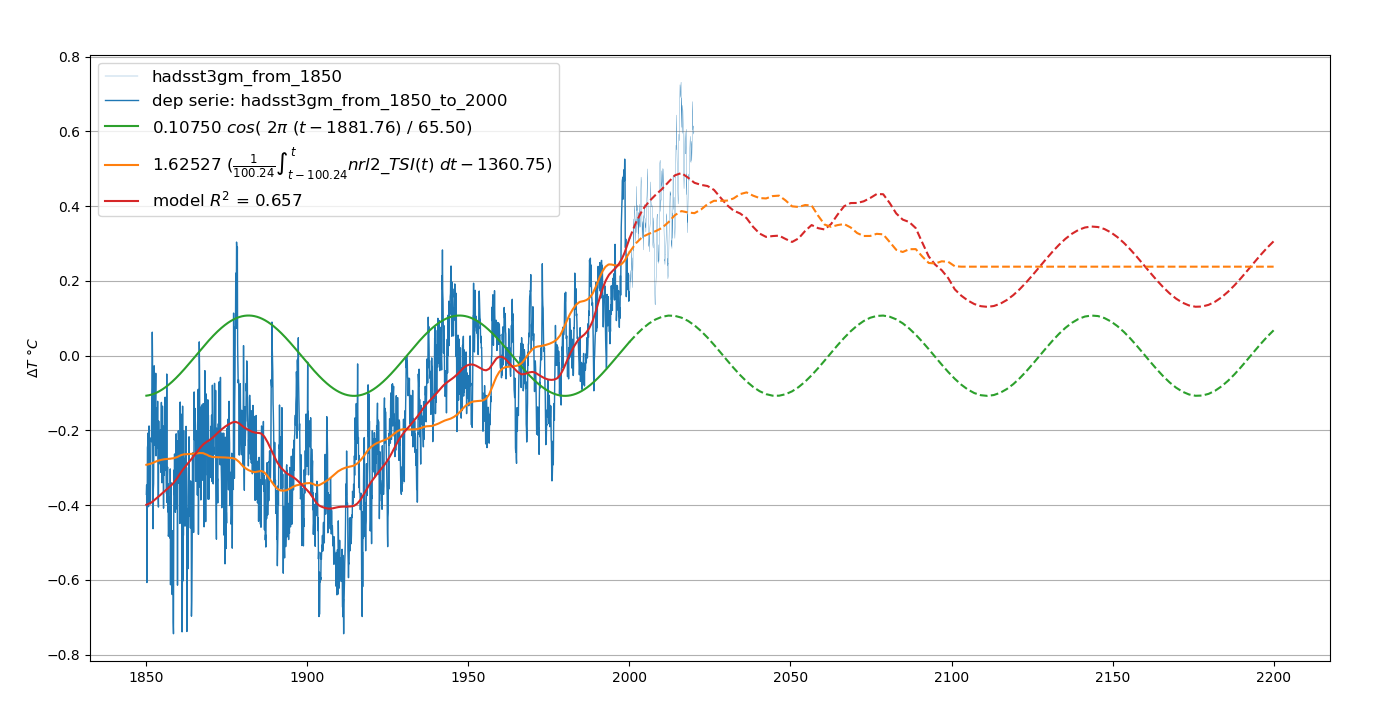
Ce résultat valide le modèle.
4.7.8 Analyse TS.7: sortie du petit âge glaciaire
C’est exactement la même analyse que l’analyse TS.5. Les données de la série nrl2 remontent jusqu’en 1610. En tenant compte de l’inertie thermique de 105 ans, l’anomalie de température peut être calculée à partir de 1715.
Ce résultat constitue une autre validation du modèle.
4.7.9 Analyses complémentaires
4.7.9.1 Mesures de la capacité prédictive des modèles
Le coefficient de détermination R2, historiquement le plus répandu, n’est pas la seule mesure utilisée pour comparer la capacité prédictive des modèles. Les statistiques CV, AIC, AICc, BIC sont également couramment utilisées. Un modèle est d’autant meilleur que son R2 est grand et que ses statistiques CV, AIC, AICc et BIC sont petites.
Ces mesures permettent de sélectionner le modèle qui a la meilleure capacité prédictive. Elles sont expliquées au chapitre 5 dans (Hyndman et Athanasopoulos 2018).
Elles ont été résumées dans la Table Table 4.9.
| Anal | CV | AIC | AICc | BIC | AdjR2 | BG Test |
|---|---|---|---|---|---|---|
| TS.1 | 0.0276524 | -6929.969 | -6929.957 | -6913.270 | 0.6441065 | ❌ |
| TS.2 | 0.0277407 | -7246.240 | -7246.228 | -7229.404 | 0.6239604 | ❌ |
| TS.3 | 0.0183328 | -8131.797 | -8131.785 | -8114.944 | 0.7580459 | ❌ |
| TS.4 | 0.0156629 | -8452.167 | -8452.147 | -8429.696 | 0.7934072 | ❌ |
| TS.5 | 0.0011843 | -13703.430 | -13703.410 | -13680.960 | 0.9810580 | ❌ |
| TS.6 | 0.0162153 | -7417.273 | -7417.251 | -7395.291 | 0.6561721 | ❌ |
Des modèles TS.1 à TS.4, il apparaît clairement que celui de l’analyse TS.4 est le meilleur, quelle que soit la statistique utilisée pour effectuer la comparaison.
Le modèle TS.5 ne peut être directement comparé avec les modèles précédents, parce qu’il a été calculé avec une anomalie de température lissée.
Le modèle TS6, qui est le modèle TS4 calculé avec des données arrêtées en l’an 2000, est repris à titre indicatif.
Les résidus des analyses échouent au test de Breusch-Godfrey (colonne BG Test). Les résidus sont analysés en détail à la Section 4.7.9.2.
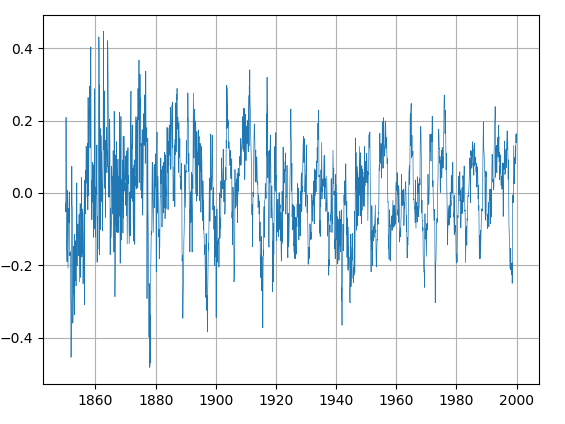
4.7.9.2 Résidus des analyses de régression
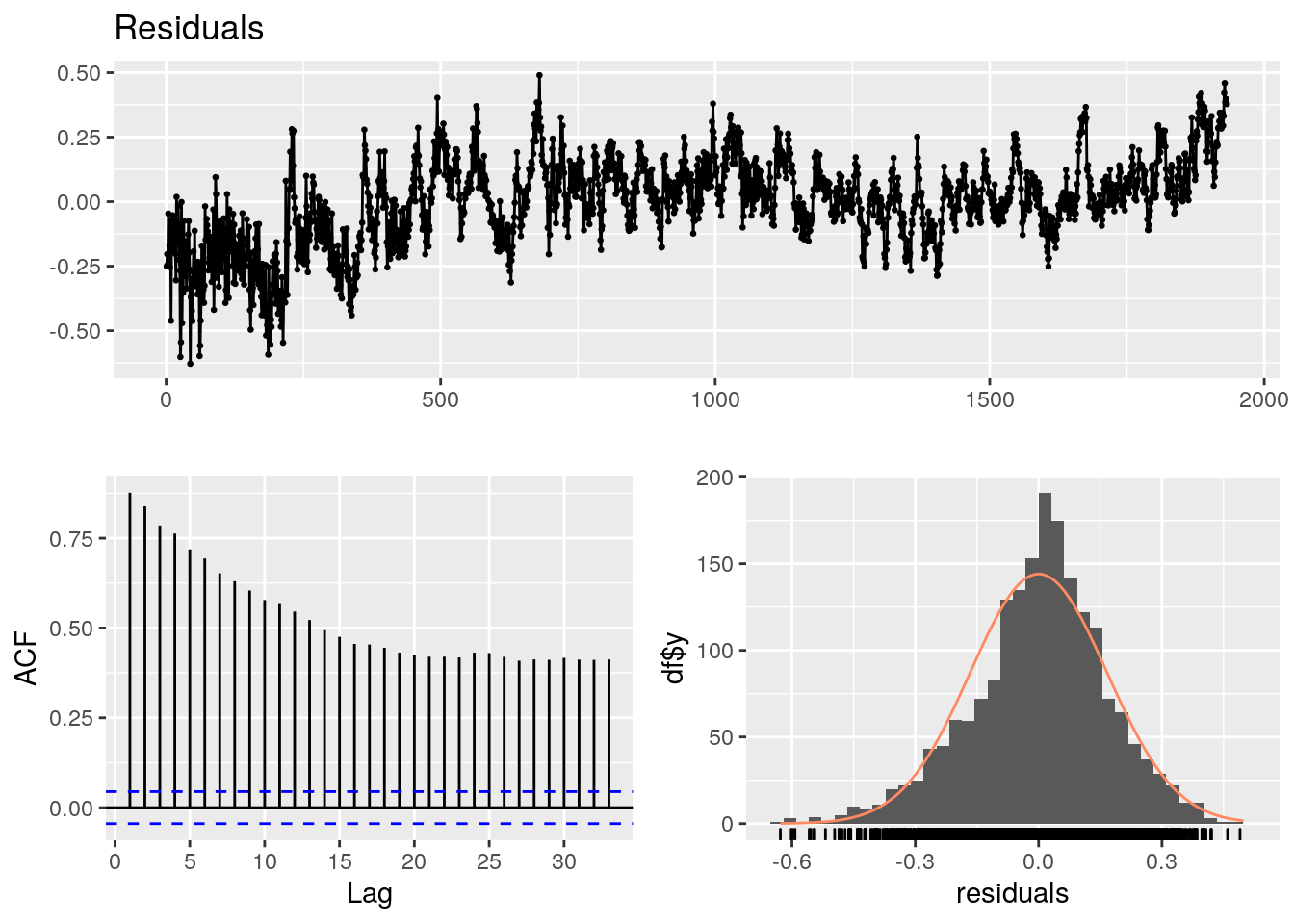
Les résidus d’une analyse de régression sont égaux à la différence entre les valeurs observées et les valeurs modélisées. La moyenne des résidus doit être nulle, et ils ne devraient pas présenter d’auto-corrélation.
Les séries utilisées dans les analyses de régression présentent souvent une tendance et de l’auto-corrélation dans leurs résidus. Cela ne signifie pas que les prédictions de ces modèles soient biaisées, mais ces prédictions pourraient être améliorées en exploitant l’information contenue dans l’auto-corrélation.
Pour apprécier la qualité des résidus, on les compare à un bruit blanc qui ne contient aucune information et aucune auto-corrélation.
95 % des coefficients du graphe d’auto-corrélation des résidus doivent être situés dans l’intervalle
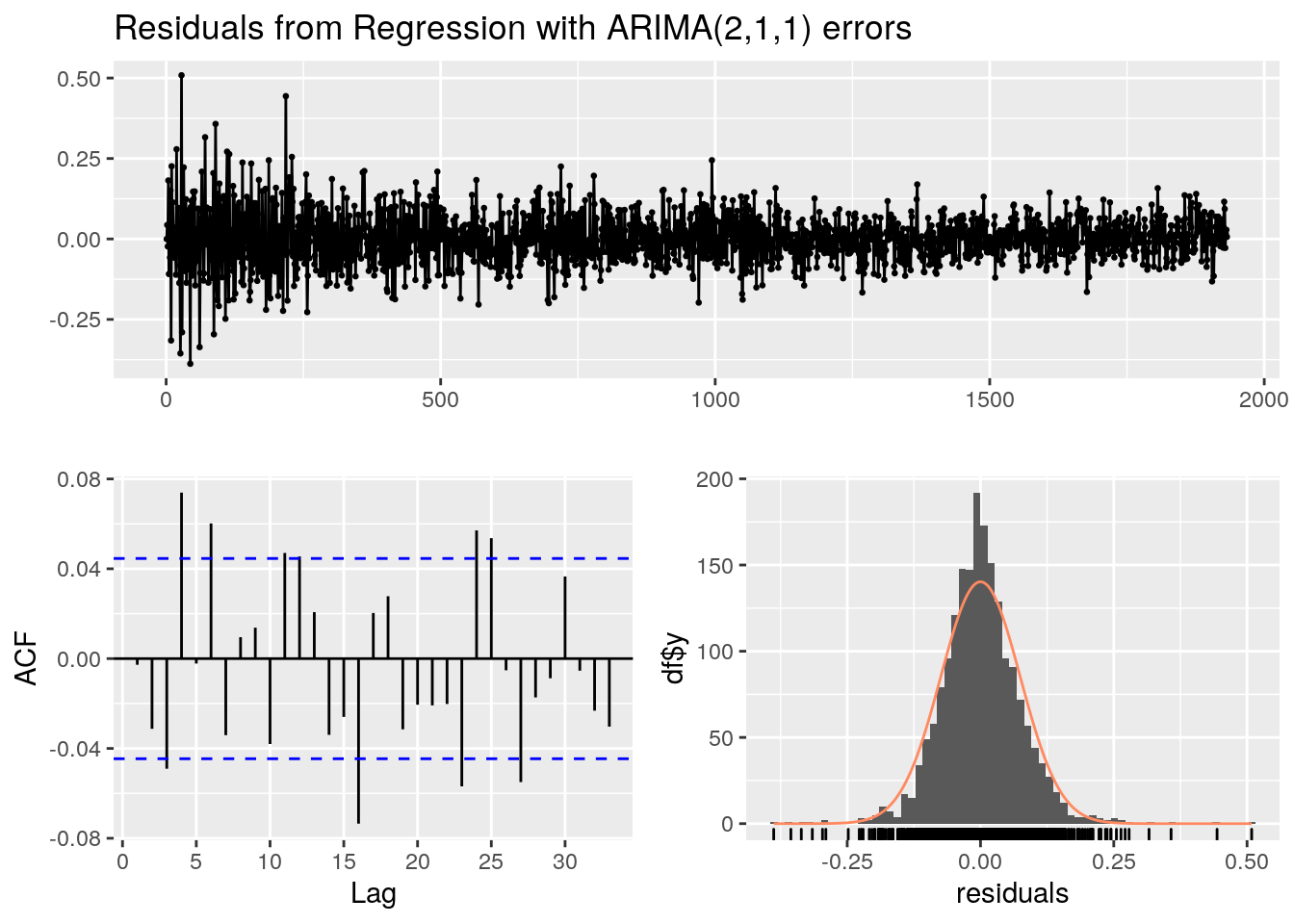
En cas d’auto-corrélation dans les résidus, on peut recourir à des modèles de régression dynamiques beaucoup plus sophistiqués, qui combinent des modèles de régression classiques et des modèles de type ARIMA, en espérant obtenir des résidus proches d’un bruit blanc qui satisfont aux tests de type portemanteau. Ces techniques de calcul sont décrites aux chapitres 8 et 9 dans (Hyndman et Athanasopoulos 2018).
Le test de Breusch-Godfrey est préféré pour les modèles de régression classiques, et celui de Ljung-Box pour les modèles de régression dynamiques. On considère qu’il y a absence d’auto-corrélation lorsque la probabilité de l’hypothèse nulle du test est supérieure à 0.05.
Tous les modèles de régression classique TS.1 à TS.4 présentent de l’auto-corrélation, et échouent au test de type portemanteau. Ils ont dès lors été complétés par un modèle de type ARIMA. Les projections de ces modèles ont été calculées en supposant que pour les 200 mois suivants, les valeurs des sunspots, irradiances totales solaires et du terme harmonique éventuel sont égales à leurs dernières observations (« naïve forecast »).
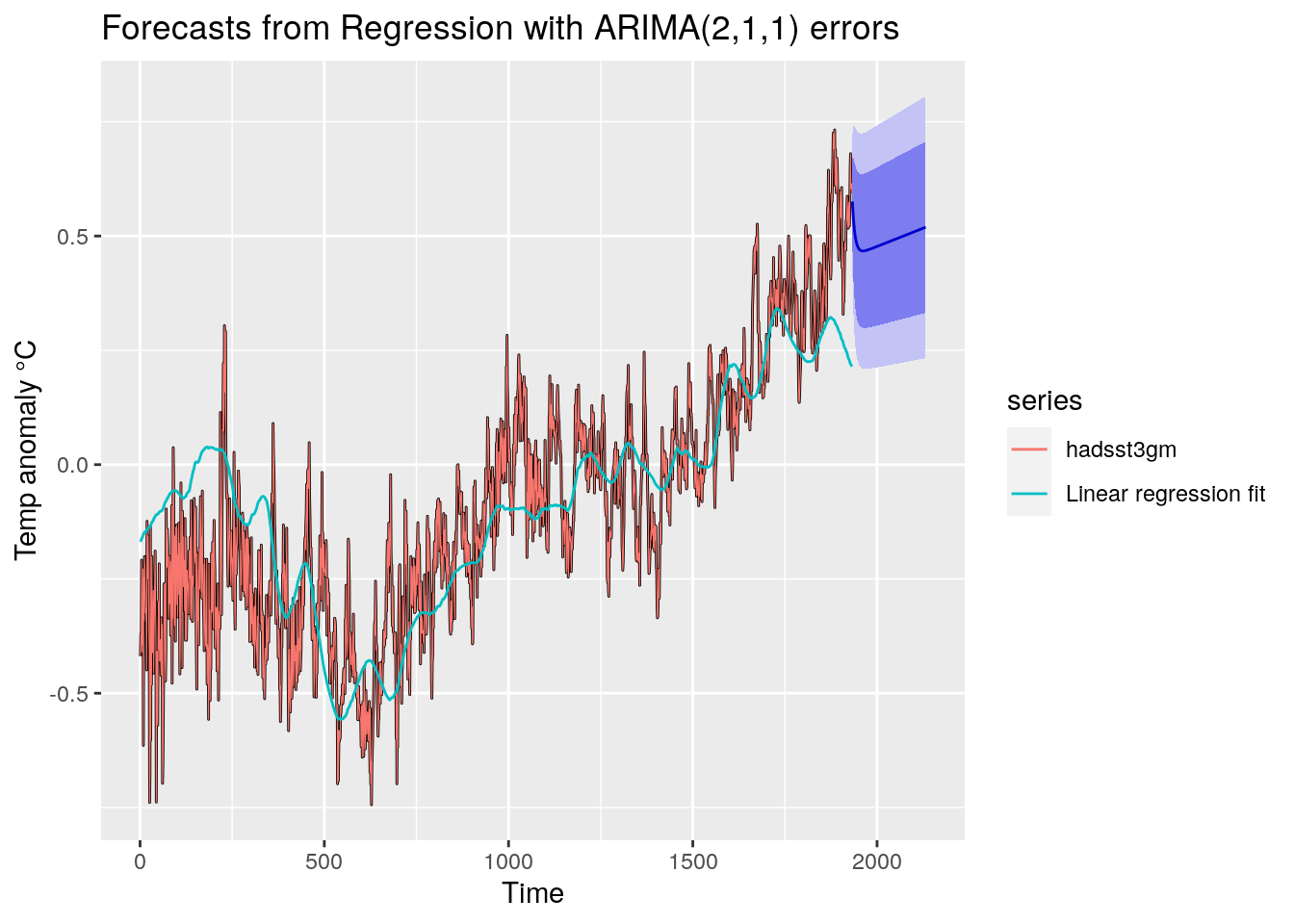
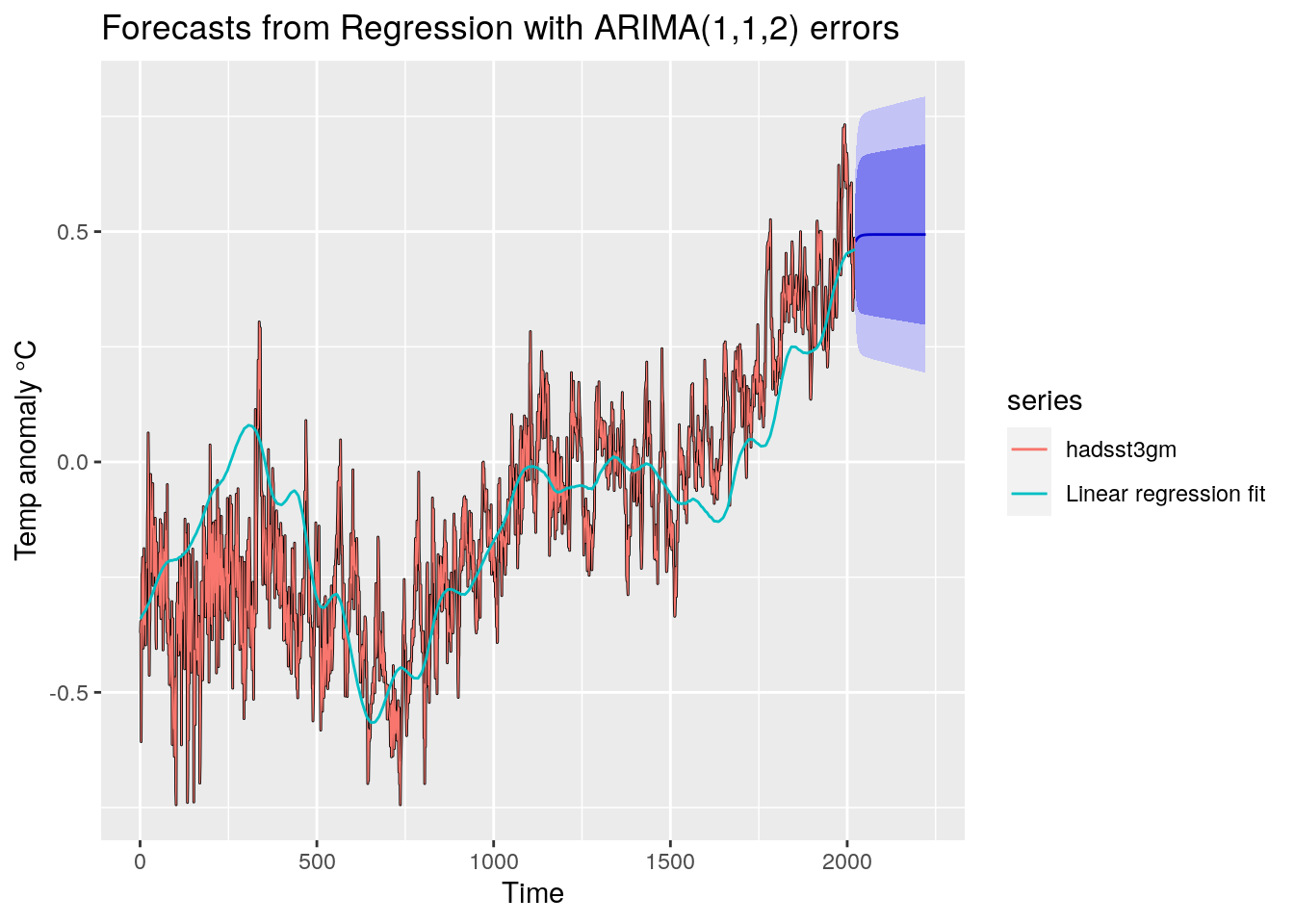
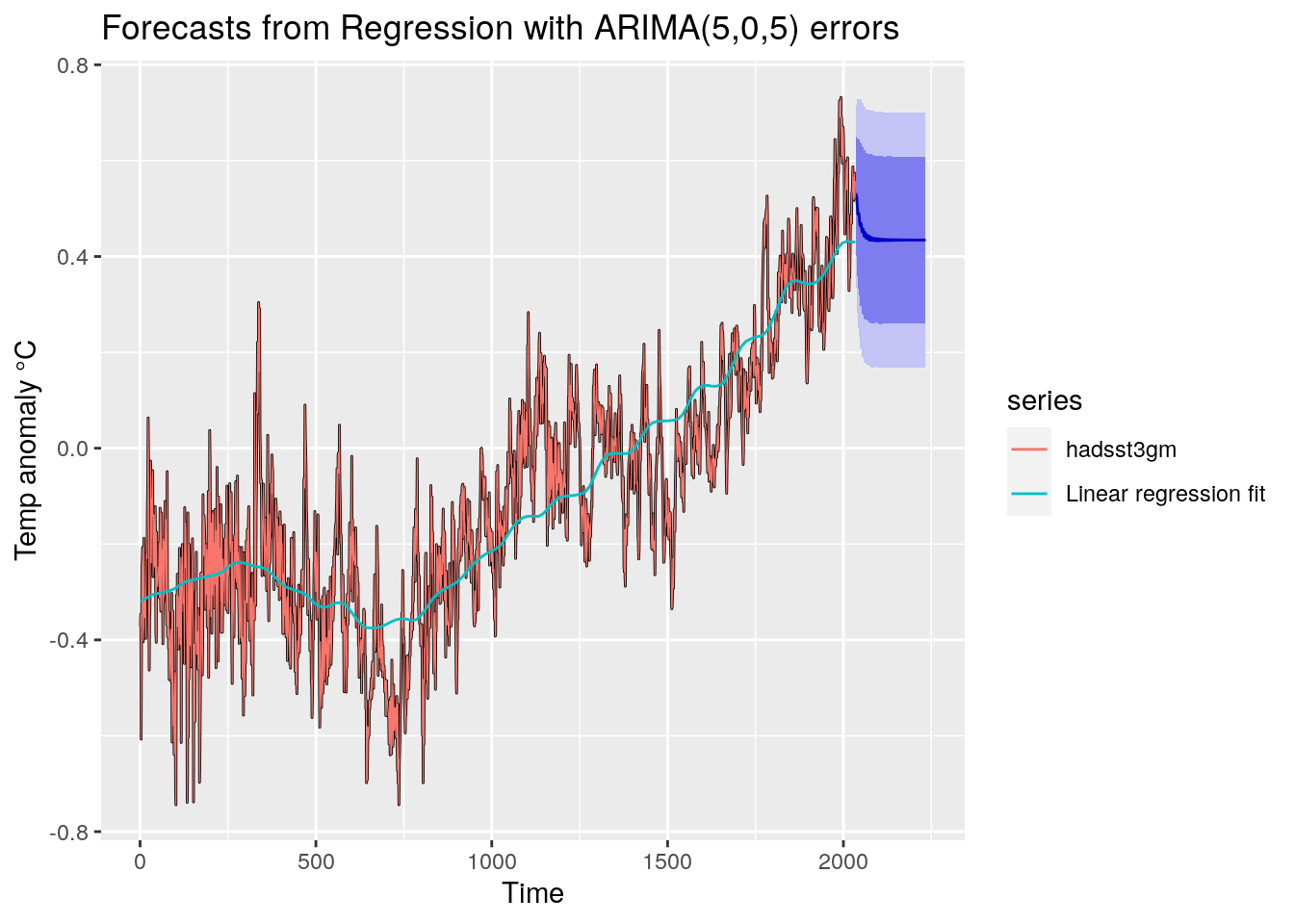
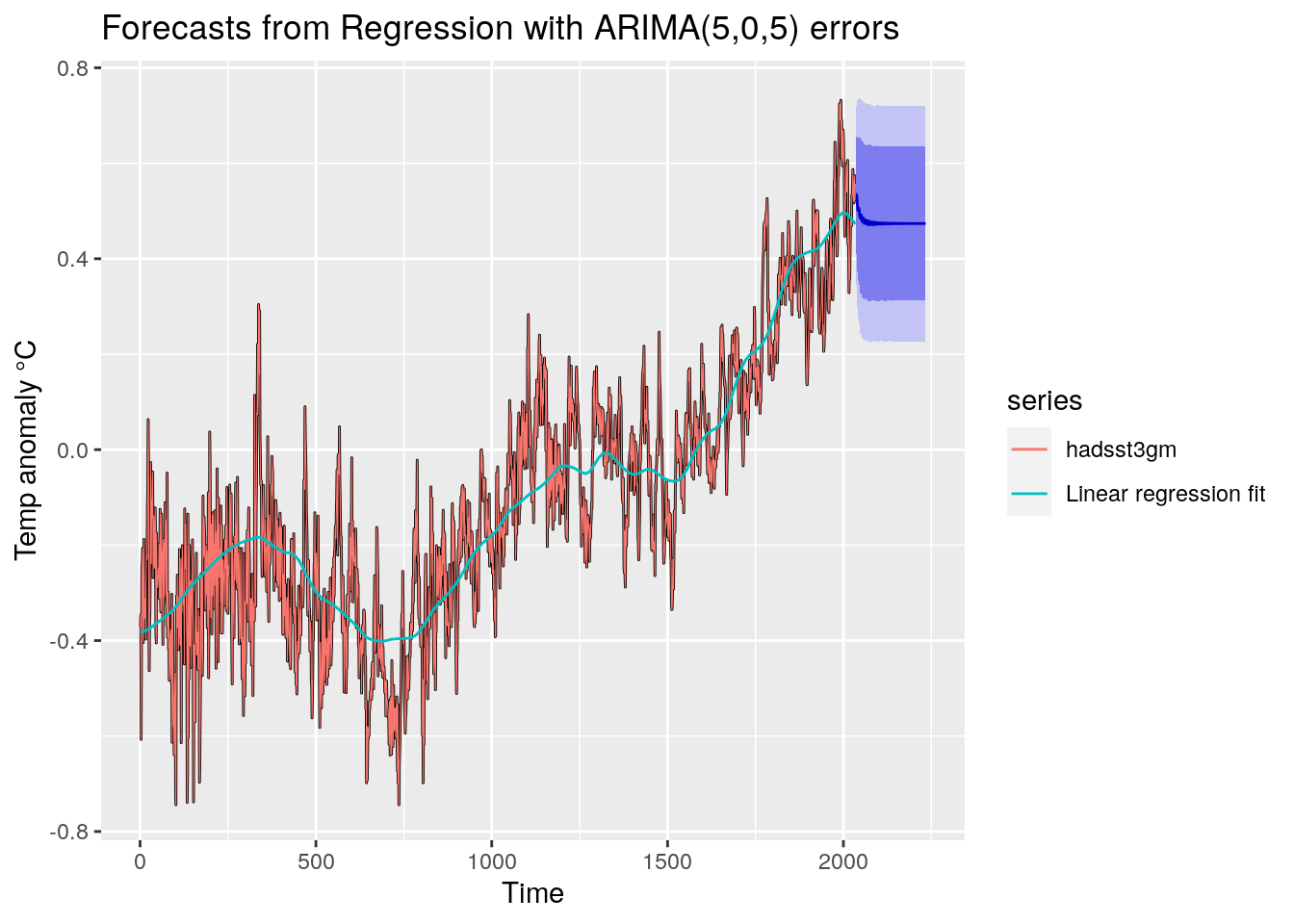
Les graphiques des analyses reprennent
en cyan, la modélisation par régression classique.
en rouge, la variable dépendante (l’anomalie de température hadsst3).
en noir, la modélisation « régression + ARIMA », qui se confond quasiment avec la courbe rouge, tellement l’ajustement est élevé.
en bleu, la projection « régression + ARIMA », avec ses intervalles de confiance à 80 % (en bleu foncé) et à 95 % en bleu clair.
Les capacités prédictives des modèles avec ARIMA sont résumées dans la Table Table 4.10.
Il apparaît clairement que le modèle TS.4 est le meilleur, quelle que soit la statistique utilisée pour effectuer la comparaison.
Le détail de ces analyses est commenté ci-dessous.
4.7.9.2.1 Analyse résidus TS.1
4.7.9.2.1.1 Sans ARIMA
##
## Breusch-Godfrey test for serial correlation of order up to 10
##
## data: Residuals
## LM test = 1539.1, df = 10, p-value < 2.2e-16Il y a une tendance dans les résidus qui sont dissymétriques. Le graphe d’auto-corrélation se stabilise à une valeur trop élevée pour satisfaire au test portemanteau.
4.7.9.2.1.2 Avec ARIMA
## regr_ar = auto.arima(df$hadsst3gm, xreg = df$sunspotsAvg)
##
## Series: df$hadsst3gm
## Regression with ARIMA(2,1,1) errors
##
## Coefficients:
## ar1 ar2 ma1 drift xreg
## 0.5649 0.2677 -0.9891 3e-04 0.5928
## s.e. 0.0225 0.0224 0.0042 1e-04 0.1308
##
## sigma^2 estimated as 0.005585: log likelihood=2270.55
## AIC=-4529.11 AICc=-4529.06 BIC=-4495.71
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE ACF1
## Training set 5.346618e-06 0.07461492 0.0550197 Inf Inf 0.9295593 -0.002741821##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(2,1,1) errors
## Q* = 87.45, df = 25, p-value = 7.426e-09
##
## Model df: 5. Total lags used: 30Il n’y a pas de tendance dans les résidus qui sont quasiment symétriques. Les coefficients d’auto-corrélation sont légèrement trop élevés pour pour être validés par le test portemanteau. Les intervalles de confiance des projections augmentent avec le temps. Le coefficient sur le nombre moyen de taches solaires (sunspotsAvg) est quasiment égal à 0.5928, ce qui invalide l’analyse correspondante sans ARIMA.
4.7.9.2.2 Analyse résidus TS.2
4.7.9.2.2.1 Sans ARIMA
##
## Breusch-Godfrey test for serial correlation of order up to 10
##
## data: Residuals
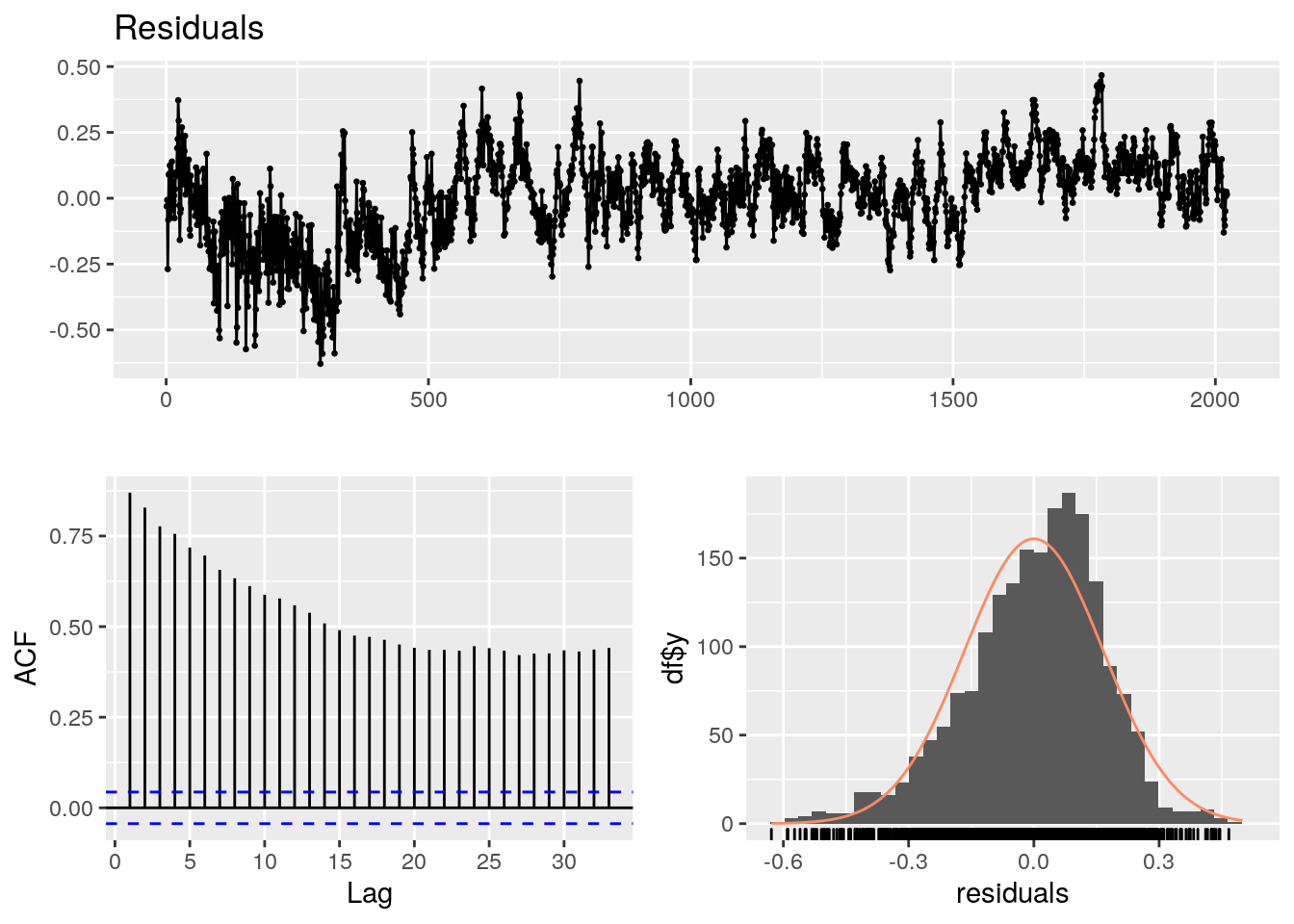
## LM test = 1583.1, df = 10, p-value < 2.2e-16Il y a une tendance dans les résidus qui sont dissymétriques. Le graphe d’auto-corrélation se stabilise à une valeur trop élevée pour satisfaire au test portemanteau.
4.7.9.2.2.2 Avec ARIMA
## regr_ar = auto.arima(df$hadsst3gm, xreg = df$histTsiAvg)
##
## Series: df$hadsst3gm
## Regression with ARIMA(1,1,2) errors
##
## Coefficients:
## ar1 ma1 ma2 xreg
## 0.8948 -1.3227 0.3300 0.6015
## s.e. 0.0144 0.0273 0.0265 0.1198
##
## sigma^2 estimated as 0.006025: log likelihood=2299.24
## AIC=-4588.48 AICc=-4588.45 BIC=-4560.42
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE ACF1
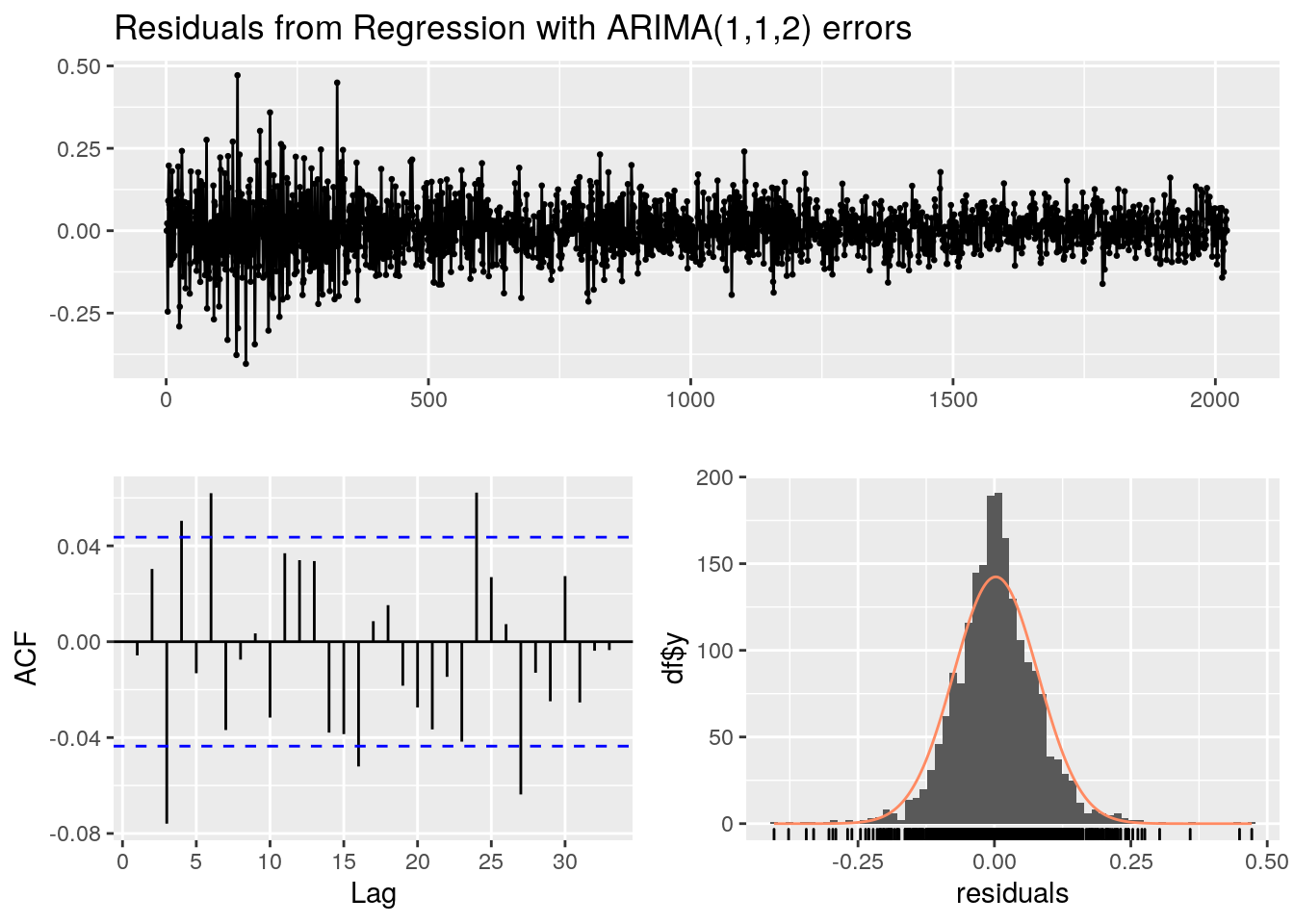
## Training set 0.002490818 0.07752253 0.05691908 Inf Inf 0.9259642 -0.005702849##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(1,1,2) errors
## Q* = 81.36, df = 26, p-value = 1.292e-07
##
## Model df: 4. Total lags used: 30Il n’y a pas de tendance dans les résidus qui sont quasiment symétriques. Les coefficients d’auto-corrélation sont légèrement trop élevés pour être validés par le test portemanteau. Les intervalles de confiance des projections augmentent avec le temps. Le coefficient sur le nombre moyen de taches solaires (histTsiAvg) est égal à 0.6015, ce qui invalide l’analyse correspondante sans ARIMA.
4.7.9.2.3 Analyse résidus TS.3
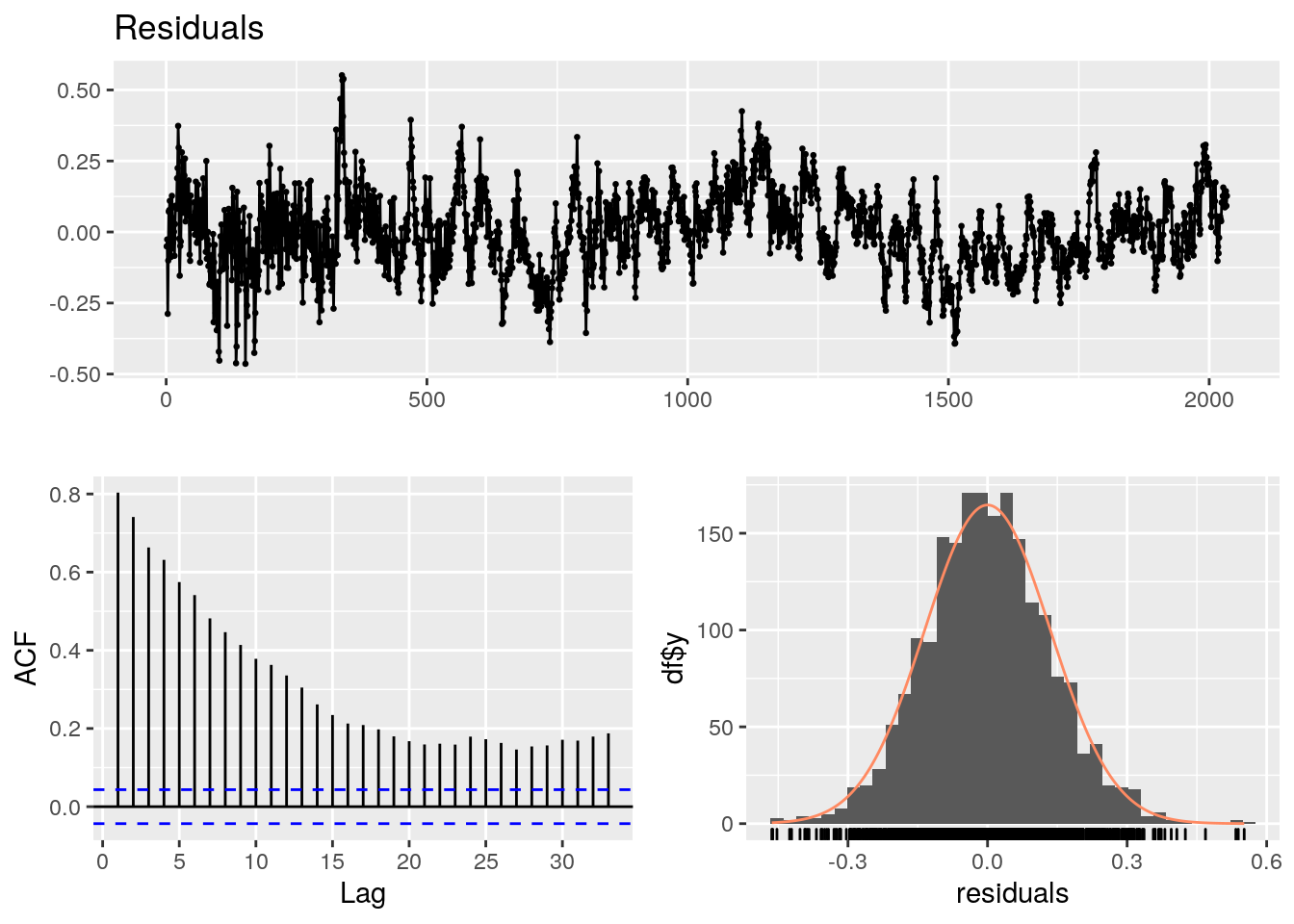
4.7.9.2.3.1 Sans ARIMA
##
## Breusch-Godfrey test for serial correlation of order up to 10
##
## data: Residuals
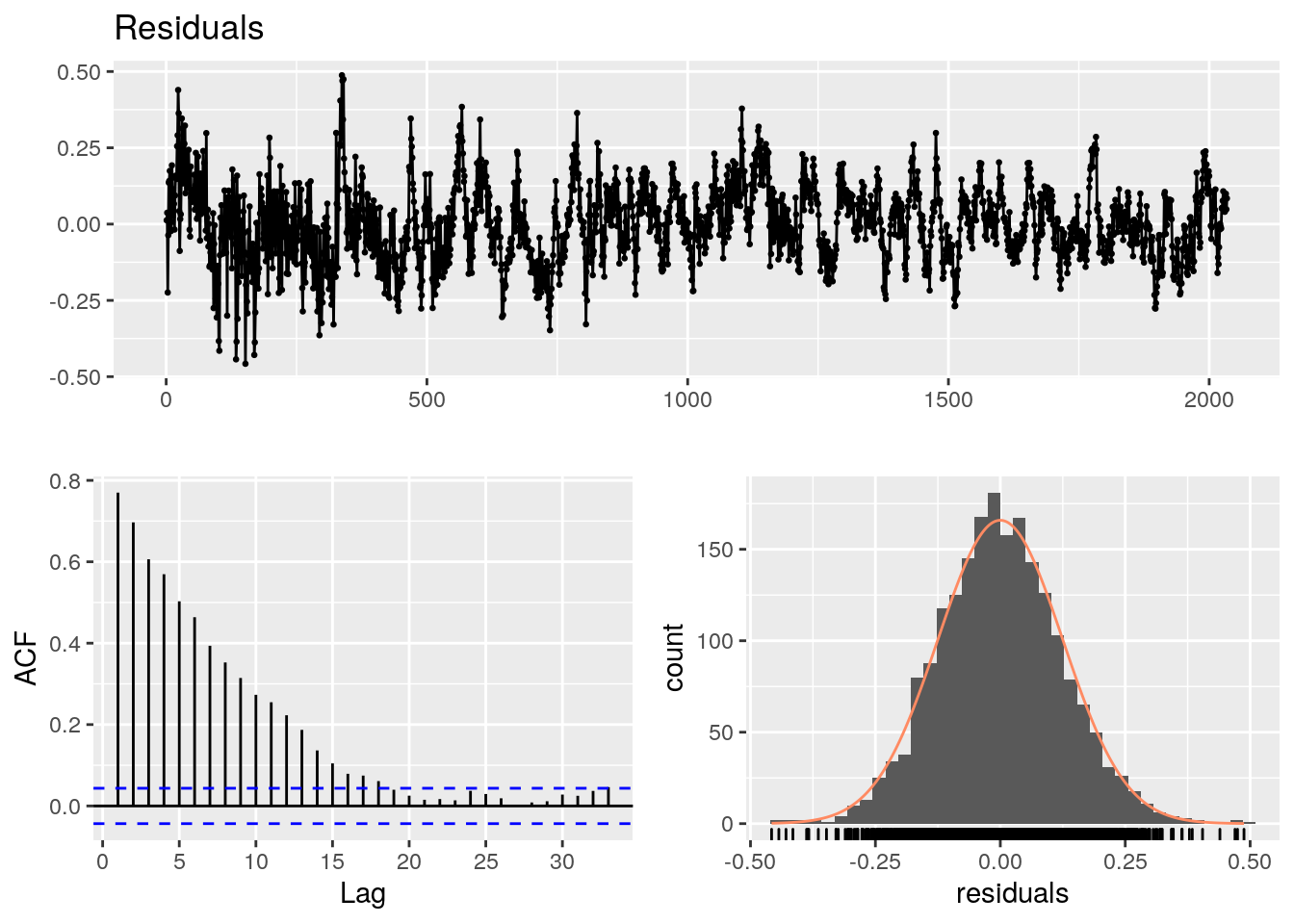
## LM test = 1377.9, df = 10, p-value < 2.2e-16Il n’y a pas de tendance dans les résidus qui sont symétriques. Le graphe d’auto-corrélation se stabilise à une valeur trop élevée pour satisfaire au test portemanteau.
4.7.9.2.3.2 Avec ARIMA
## regr_ar = auto.arima(df$hadsst3gm, xreg = df$nrl2TsiAvg)
##
## Series: df$hadsst3gm
## Regression with ARIMA(5,0,5) errors
##
## Coefficients:
## ar1 ar2 ar3 ar4 ar5 ma1 ma2 ma3 ma4
## 0.0653 0.7917 -0.8496 -0.1234 0.8227 0.5105 -0.2809 0.7922 0.6033
## s.e. 0.3650 0.1537 0.0650 0.0743 0.3516 0.3736 0.3607 0.3726 0.1146
## ma5 intercept xreg
## -0.2623 0.0011 1.0080
## s.e. 0.2686 0.0147 0.0562
##
## sigma^2 estimated as 0.005875: log likelihood=2343.56
## AIC=-4661.13 AICc=-4660.95 BIC=-4588.1
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE ACF1
## Training set 5.937753e-05 0.0764199 0.05646927 Inf Inf 0.9215865 -0.001125632##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(5,0,5) errors
## Q* = 24.086, df = 18, p-value = 0.1522
##
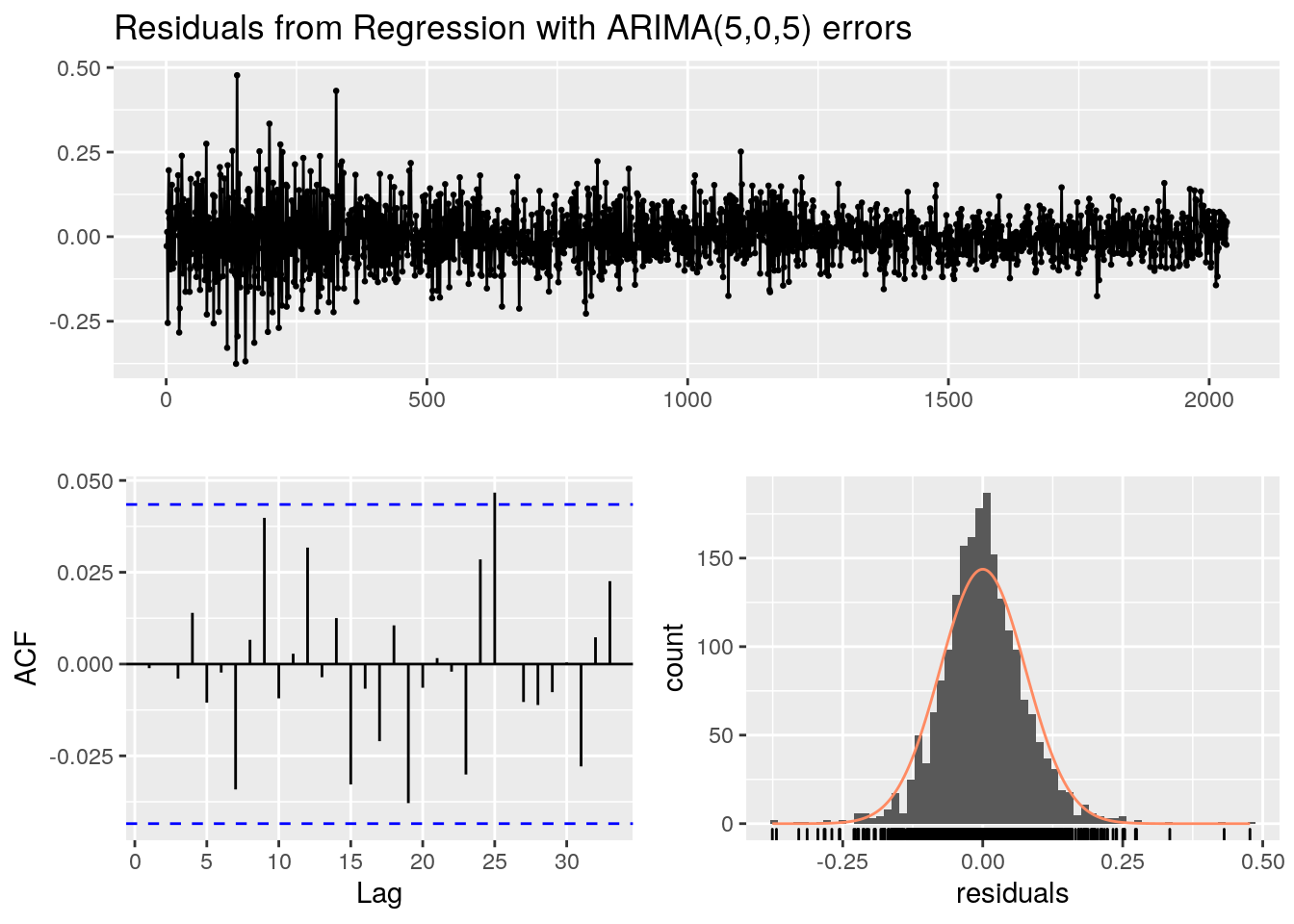
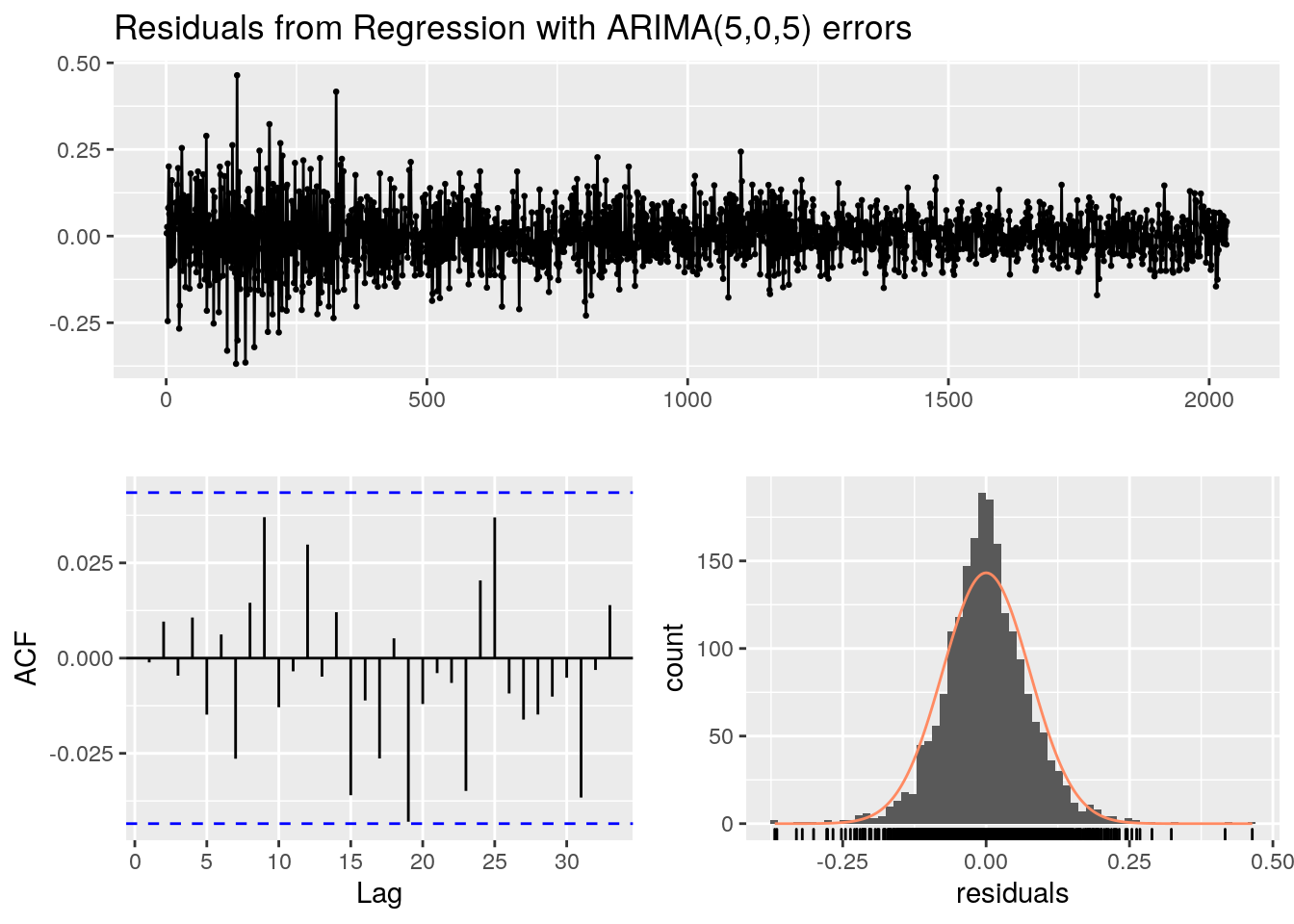
## Model df: 12. Total lags used: 30Il n’y a pas de tendance dans les résidus qui sont quasiment symétriques. Les coefficients d’auto-corrélation restent dans les limites admises et sont validés par le test portemanteau. Les intervalles de confiance des projections sont constants. La déviation standard de la projection est égale à celle des données historiques. Le coefficient sur l’ITS moyenne (nrl2TsiAvg) est quasiment égal à 1, ce qui valide l’analyse correspondante sans ARIMA.
4.7.9.2.4 Analyse résidus TS.4
4.7.9.2.4.1 Sans ARIMA
##
## Breusch-Godfrey test for serial correlation of order up to 10
##
## data: Residuals
## LM test = 1272.5, df = 10, p-value < 2.2e-16Il n’y a pas de tendance dans les résidus qui sont symétriques. Le graphe d’auto-corrélation finit par rentrer dans les limites admises, mais le test portemanteau n’est pas satisfait.
4.7.9.2.4.2 Avec ARIMA
## regr_ar = auto.arima(df$hadsst3gm, xreg = cbind(df$harm,df$nrl2TsiAvg))
##
## Series: df$hadsst3gm
## Regression with ARIMA(5,0,5) errors
##
## Coefficients:
## ar1 ar2 ar3 ar4 ar5 ma1 ma2 ma3 ma4
## 0.0671 0.8154 -0.8652 -0.1736 0.8043 0.4997 -0.3293 0.7787 0.6393
## s.e. 0.0203 0.0334 0.0350 0.0329 0.0285 0.0296 0.0574 0.0264 0.0397
## ma5 xreg1 xreg2
## -0.2422 1.0041 1.0019
## s.e. 0.0326 0.1620 0.0451
##
## sigma^2 estimated as 0.005821: log likelihood=2352.91
## AIC=-4679.82 AICc=-4679.64 BIC=-4606.79
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE ACF1
## Training set 7.192395e-05 0.07607203 0.05621399 Inf Inf 0.9174202 -0.00112353925632##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(5,0,5) errors
## Q* = 24.389, df = 18, p-value = 0.1427
##
## Model df: 12. Total lags used: 30Il n’y a pas de tendance dans les résidus qui sont quasiment symétriques. Les coefficients d’auto-corrélation restent dans les limites admises et sont validés par le test portemanteau. Les intervalles de confiance des projections sont constants. La déviation standard de la projection est égale à celle des données historiques. Les coefficients sur le terme harmonique (harm) et sur l’ITS moyenne (nrl2TsiAvg) sont quasiment égaux à 1, ce qui valide l’analyse correspondante sans ARIMA.
4.7.10 Projections d’activité solaire et de température
Pour tester la capacité prédictive du modèle, il faut disposer de projections de l’intensité solaire, ou de son proxy, l’irradiance. Différents modèles théoriques d’irradiance ont été développés.
4.7.10.1 Modèles projectifs d’activité solaire
Le modèle de (Salvador 2013) est fondé sur les conjonctions des planètes qui influencent les orbites terrestres et l’activité solaire, qui dépendrait de la position du soleil par rapport au centre de gravité du système solaire. Les constantes du modèle sont disponibles à cette adresse. Sa reconstruction des taches solaires depuis l’an 1000 reconstitue fidèlement les minima historiques (Voir Figure 1.2). Salvador considère que son modèle est précis pour les 2 ou 3 prochains cycles solaires et devrait donner une bonne projection pour les 100 prochaines années qui devraient voir un grand minimum solaire, et donc aussi une mini-période glaciaire.
Voir Figure 4.45.
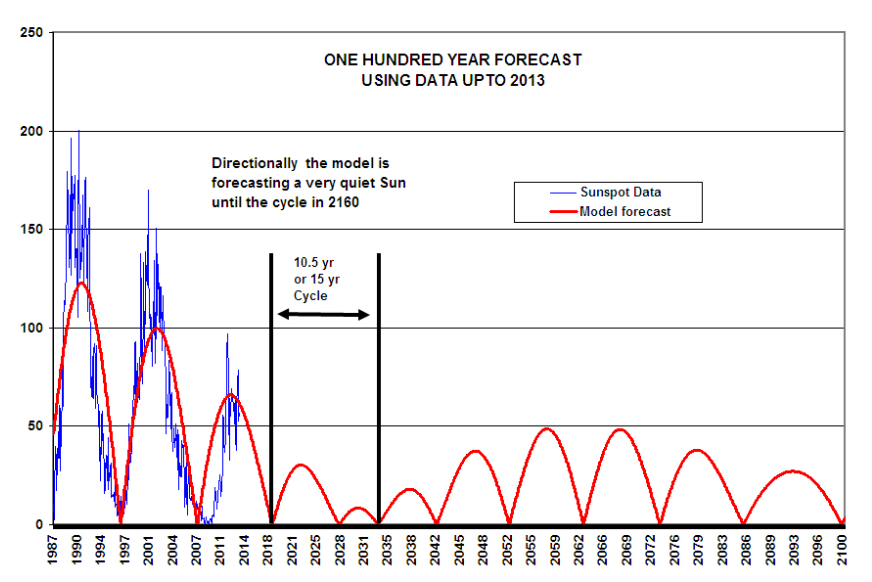
Le modèle de (Zharkova et al. 2015) est basé sur une analyse détaillée du champ magnétique solaire des cycles solaires 21 à 24. Le champ magnétique solaire découlerait de la somme de 2 composantes ayant des fréquences proches produisant une modulation dont la période est d’environ 350 ans qui se superpose à un cycle d’environ 22 ans (deux fois la durée du cycle de Schwabe). Cette période de 22 ans correspond à une inversion des pôles magnétiques du soleil. L’allure des variations de ce champ magnétique présente une ressemblance remarquable avec les taches solaires et reproduit également leurs minima historiques. Voir Figure 1.3. Zharkova considère que son approche ouvre une nouvelle ère dans la projection de l’activité solaire à l’échelle du millénaire. Elle pense également que nous nous dirigeons vers un grand minimum solaire.
Dans (Velasco Herrera, Mendoza, et He 2015) il y a deux reconstructions de l’irradiance totale solaire (ITS) depuis l’an 1000 avec des projections jusqu’en 2100. Ces reconstructions ont été calibrées sur base des composites PMOD et ACRIM qui utilisent des algorithmes différents pour calculer l’ITS. L’ITS PMOD est la plus récente. Le satellite à la base de l’ITS ACRIM n’est plus opérationnel. Il n’y a pas eu de période de recouvrement permettant de calibrer les mesures du dernier satellite avec le précédent. Les spécialistes ne sont pas d’accord entre eux quant à la manière de raccorder les séries de mesures. Les périodes et durées des grand minima historiques se retrouvent dans chaque reconstruction de Velasco, avec peu de différences entre elles.
4.7.10.2 Projections de température
Dans le présent travail, des calculs de régression analogues à ceux des analyses TSx ont été effectués pour les modèles de Salvador et Velasco. Les données publiées du modèle de Zharkova contiennent trop peu d’informations pour le faire. Un terme harmonique a été utilisé dans chacune des analyses.
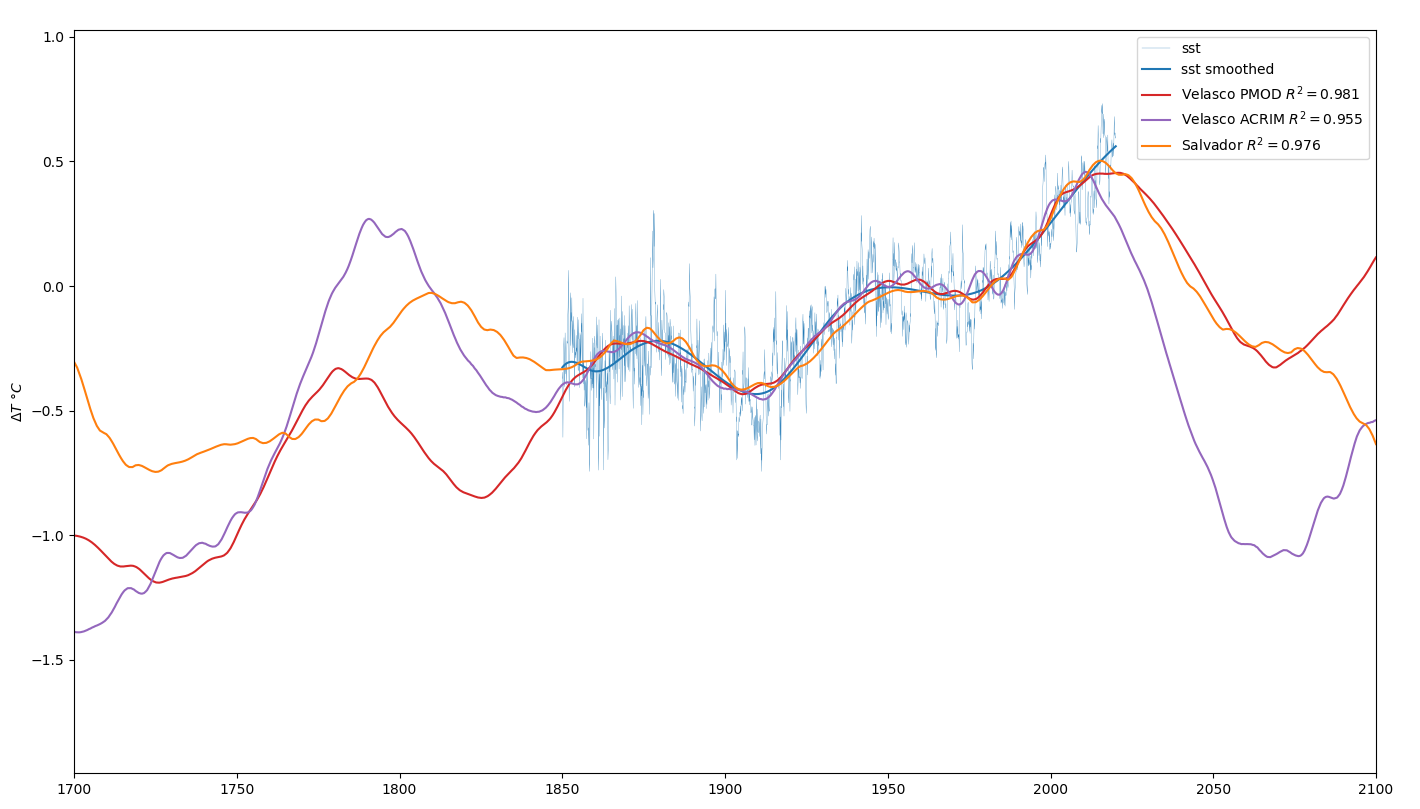
Les modélisations présentent toutes un coefficient de corrélation fort élevé, ce qui ne les empêche pas d’être sensiblement différentes lorsqu’on sort de l’intervalle d’observation. Ce résultat confirme qu’il est beaucoup plus difficile d’extrapoler des données que de les interpoler. Les projections que l’on peut faire à un siècle doivent donc être considérées avec toutes les réserves d’usage, et cela quelle que soit la méthode utilisée pour les calculer.
Moyennant ces réserves, on constate que les trois simulations prédisent, à des degrés divers, un refroidissement pour les décennies à venir. La diminution de température jusqu’en 2070 devrait être (au moins) aussi rapide que l’augmentation de température encourue à la fin du siècle dernier. A cet horizon, la température serait redevenue semblable à celle du début du siècle passé, voire beaucoup plus basse, et cela de manière purement naturelle, sans aucune intervention humaine.
Ces résultats sont conformes aux avis d’une longue liste d’auteurs (Voir (Mörner 2015)) pour lesquels un refroidissement significatif, voire un nouveau petit âge glaciaire doit être envisagé, plutôt qu’un réchauffement catastrophique, tel qu’annoncé par le GIEC.