1 Introduction

1.1 L’état des connaissances orthodoxes et hétérodoxes

Le GIEC utilise un modèle statique du climat qui peut se résumer comme suit:

le climat se serait stabilisé avant l’époque pré-industrielle.
le rayonnement solaire n’a quasiment pas changé depuis lors.
l’augmentation du taux de CO₂ atmosphérique est exclusivement d’origine anthropique et découle uniquement de l’usage de combustibles fossiles.
cette contribution anthropique aux émissions de CO₂ est discernable des contributions naturelles, en utilisant la signature isotopique comme marqueur.
cette augmentation du CO₂ est la seule cause de l’augmentation de la température par le biais d’un « effet de serre atmosphérique » radiatif.
les contributions naturelles (nuages, aérosols, etc.) sont considérées comme des “forcings”, que l’on peut associer mathématiquement à des rétroactions positives ou négatives, qui respectivement amplifient ou amortissent “l’effet de serre atmosphérique”.
dans ses modèles dits de circulation globale, le système climatique est localement à l’équilibre et les transferts de matière et chaleur entre cellules locales sont définis par les équations de Navier-Stokes.

Le GIEC ignore complètement la variation climatique liée aux variations d’intensité du rayonnement solaire, un phénomène qui a toujours existé, et ne cherche qu’à prouver, conformément à ses statuts et à son mandat, que l’activité humaine est la seule cause du réchauffement climatique.

Les suppôts du GIEC se plaisent à rappeler que malgré de nombreux efforts, personne n’a présenté une alternative valable à ce modèle. On vit dans un monde où prévaut une logique inversée. Ceux qui pensent que le soleil continue à agir comme il l’a toujours fait doivent le prouver, alors que les projections faites à partir des modèles du GIEC, admises par consensus obtenu parmi ses membres, ont toujours été contredites par les observations.

Avec ces hypothèses qui heurtent le bon sens, le GIEC ne peut que faire sienne la citation de Confucius « Vous ne trouverez pas ce que vous ne cherchez pas ». Le soleil est la première source d’énergie de notre planète et est la cause des variations de température que nous observons, qu’elles soient journalières, annuelles ou sur de plus longues périodes. A toutes les échelles de temps, l’activité solaire varie et a un impact majeur sur la température terrestre.

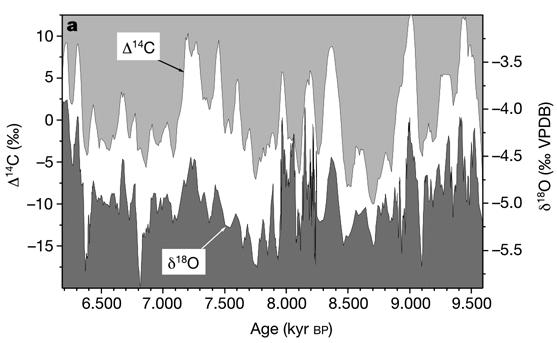
Nir Shaviv, un scientifique israélien, montre sur son blog cette impressionnante corrélation entre l’activité solaire et la température (Shaviv, s. d.). Voir Figure 1.1

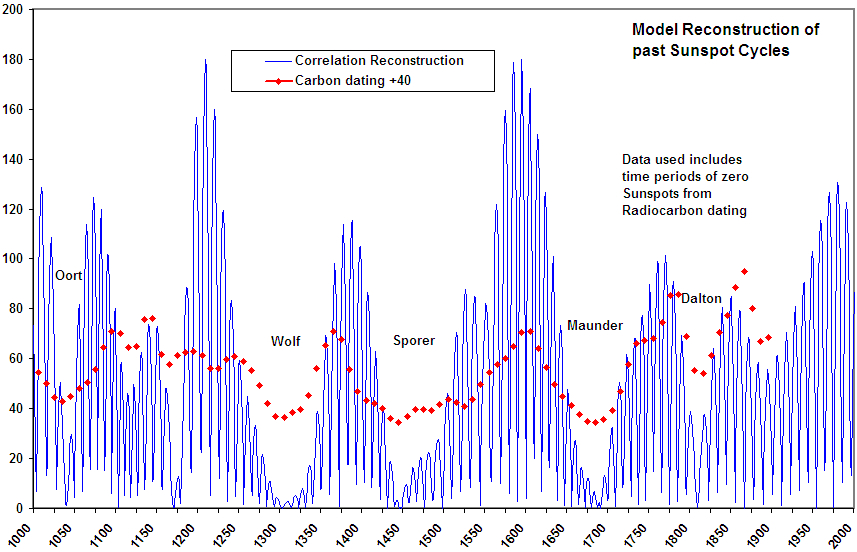
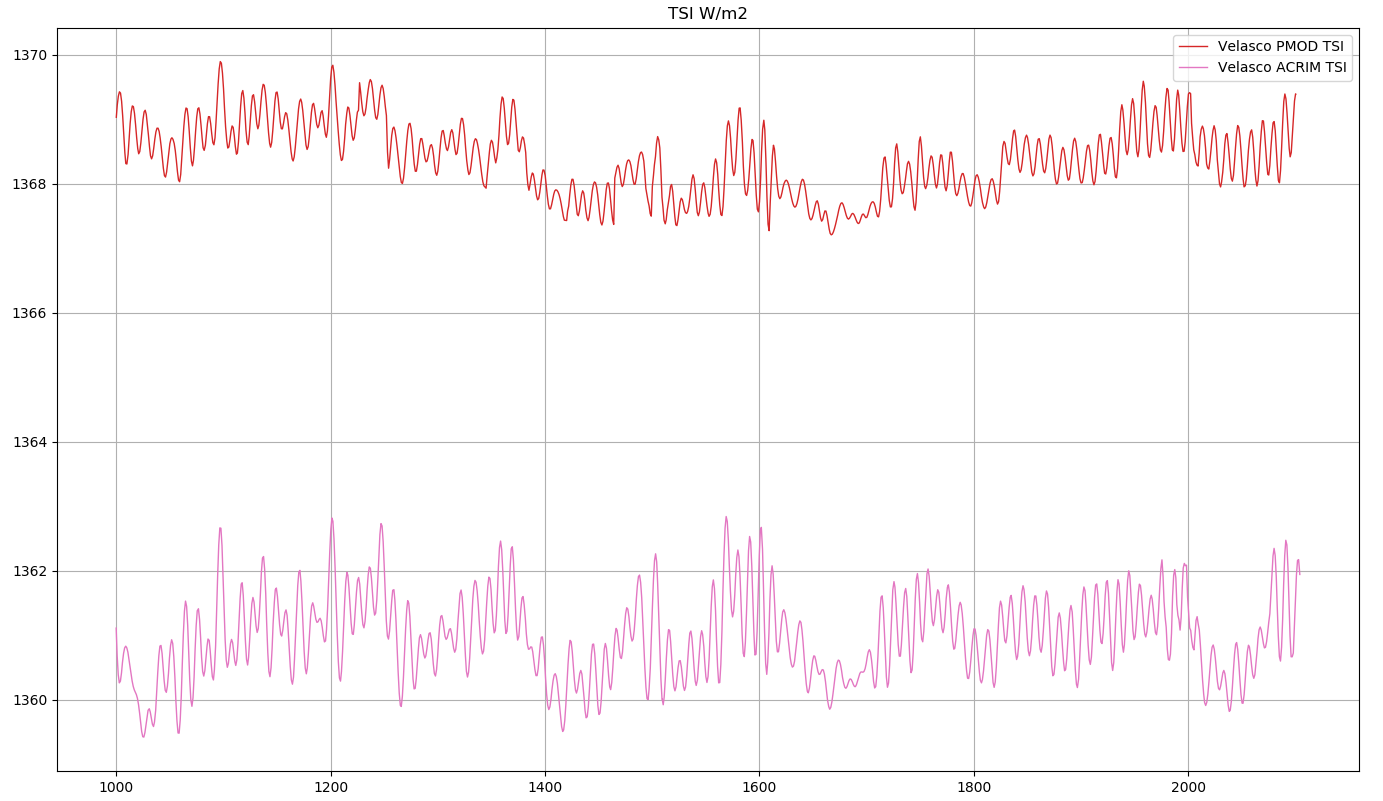
Figure 1.1: Cette figure montre l’importante corrélation entre un marqueur de l’activité solaire (\(\Delta^{14}C\)) et un marqueur de la température (\(\delta^{18}O\)). Mesures effectuées sur des stalagmites dans une grotte à Oman.

Des modélisations de l’activité solaire effectuées par (Salvador 2013) , (Zharkova et al. 2015) et (Velasco Herrera, Mendoza, et He 2015), correspondent très bien aux phases climatiques chaudes et froides des 1000 dernières années. Voir Figure 1.2, Figure 1.3 et Figure 1.4.

Plus récemment, nous avons connu un grand maximum solaire à la fin du siècle dernier, mais depuis lors, l’intensité solaire ne cesse de diminuer, et, si le soleil est le moteur du climat, nous sommes vraisemblablement en route vers des temps plus froids. L’avenir nous le dira.

Figure 1.2: Comparaison d’une modélisation du nombre de taches solaires et d’une reconstruction par datation au Carbone. En abscisse, l’année calendaire et en ordonnée, le nombre de taches solaires.

Figure 1.3: Modélisation de l’activité solaire qui reprend également les phases climatiques chaudes et froides depuis l’an 1200 et une projection jusqu’en 3200.

Figure 1.4: Reconstructions PMOD et ACRIM de l’irradiance totale solaire depuis l’an 1000 avec projections jusqu’en 2100. Depuis 1978, plusieurs satellites ont évalué l’irradiance totale solaire. Le problème, c’est qu’elle n’est pas mesurée directement, mais calculée est utilisant des techniques de calibration et des algorithmes mathématiques qui ne sont pas les mêmes dans les versions PMOD et ACRIM. Il y a des discordances entre ces versions, et les spécialistes ne sont pas d’accord entre eux. En abscisse, l’année calendaire et en ordonnée, l’irradiance totale solaire.

L’impact considérable du soleil sur le climat est évident, mais comment le quantifier ?

En adoptant comme le GIEC une approche statique du climat, on arrive à la conclusion que la variation du rayonnement solaire ne peut justifier qu’une très faible variation de température.

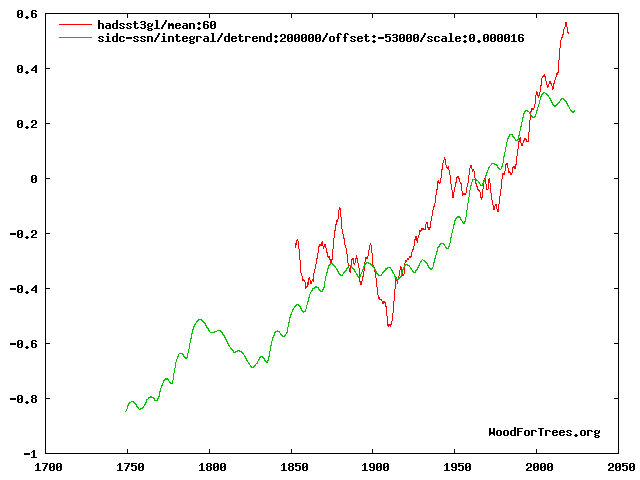
Par contre, si l’effet du rayonnement solaire sur la température résulte, non pas de ses variations, mais de son accumulation, alors il peut causer d’importantes variations de température, qui suivent de près les résultats expérimentaux. Voir Figure 1.5

Figure 1.5: L’intégrale du rayonnement solaire, mesuré par le nombre mensuel de taches solaires, peut expliquer une différence de température importante. La corrélation n’est pas mauvaise. En abscisse, l’année calendaire et en ordonnée, l’anomalie de température (°C). Voir ici

1.2 Les périodicités naturelles

Les fluctuations naturelles de température ont suscité l’intérêt des chercheurs depuis de nombreuses années, et diverses théories ont été avancées pour les expliquer :

conjonctions-oppositions de planètes et de la Lune modifiant le champ gravitationnel
position du soleil par rapport au centre de masse du système solaire, induisant un moment angulaire et des « torsions » entre les diverses couches du Soleil ce qui modifie son activité
dynamique de la « dynamo solaire », orbites de la Terre autour du soleil (les cycles de Milankovich) et l’inclinaison de son axe de rotation
des cycles liés aux courants convectifs des océans.

Des périodicités climatiques remarquables ont été mentionnées par de nombreux auteurs.

Par exemple (Scafetta 2013; Christiansen et Ljungqvist 2012; Abdussamatov 2004; Charvátová et Hejda 2014; Yndestad et Solheim 2017)

Ces cycles naturels ne sont pas toujours exactement périodiques, ce qui complique leur détection et traduit le caractère légèrement chaotique du système solaire.

1.3 La présente approche

Dans le présent travail, un modèle est proposé, qui est basé sur une corrélation très forte identifiée entre la température de surface des océans d’une part, et le rayonnement solaire moyenné sur une période mobile relativement longue (une centaine d’années), auquel on ajoute un terme harmonique indépendant de l’activité solaire, et supposé lié à des échanges de chaleur entre parties chaudes et froides, superficielles ou profondes de l’océan.

Le modèle est très simple. Le rayonnement solaire est décrit par 3 paramètres. 3 autres paramètres sont utilisés pour le terme harmonique qui ne fait qu’ajouter une oscillation sinusoïdale de la température en fonction du temps. Celle-ci n’a donc aucune influence à long terme sur le “climat”. La période de ce terme harmonique a été évaluée à environ 66 ans par analyse de régression multiple non linéaire, et confirmée par une analyse spectrale de l’anomalie de température. Ceci correspond à une périodicité climatique bien documentée. Voir notamment (Scafetta 2021).

Stockwell décrit une analyse assez semblable à la nôtre (Stockwell 2011). Il montre une bonne corrélation entre une intégrale du rayonnement solaire à partir d’un temps fixe arbitraire et l’anomalie de température pour la période de 1900 à nos jours.

Par une analyse de corrélation croisée, il trouve un décalage de 2.75 ans entre la température et le rayonnement solaire. L’intégrale d’un signal sinusoïdal est un autre signal sinusoïdal décalé du quart de sa période. La sinusoïde correspondant au modèle cumulatif proposé serait donc de 11 ans, une périodicité d’activité solaire bien documentée (cycle de Schwabe). Le signal de l’anomalie de température contient donc la signature des cycles solaires intégrés.

L’approche suivie dans le présent travail est très voisine de celle de Stockwell. Un paramètre a été ajouté pour remplacer l’intégrale depuis un temps fixe par un lissage de l’activité solaire sur une période mobile et de faire ensuite une analyse de régression multiple non linéaire, au lieu d’une analyse classique linéaire. Ceci permet d’obtenir une meilleure corrélation pour le relevé complet de température depuis 1850 jusqu’à nos jours, tout en confirmant le décalage de 2.75 ans mentionné par Stockwell.

1.4 Conséquences pour la théorie de l’effet de serre atmosphérique et son origine anthropique.

En recourant aux théories éculées d’effet de serre de Fourier et d’ Arrhenius que le temps avait enfouies dans l’oubli, le GIEC veut nous faire croire que c’est la concentration en CO₂ qui détermine la température. Mais dans ce cas, compte tenu de la très bonne corrélation entre l’activité solaire moyennée et la température, il en résulterait que la température devrait être la cause et non l’effet du rayonnement solaire, ce qui est un non-sens évident. Même si corrélation n’implique pas toujours causalité, son absence est rédhibitoire; il s’agit d’une condition nécessaire mais pas suffisante. Une autre condition (nécessaire, mais pas suffisante) est l’antériorité : une cause doit toujours précéder ou être synchrone avec un effet. Or, l’analyse de corrélation croisée montre que l’activité solaire moyennée précède la température. Il est donc impossible que la température contrôle l’activité solaire. Ceci constitue en quelque sorte une justification épistémologique de ce que le bon sens nous indique.

Cette contradiction n’est pas envisagée par le GIEC qui considère que l’augmentation de température depuis la période pré-industrielle est exclusivement d’origine anthropique, sans se demander si l’augmentation de la concentration en CO₂ atmosphérique précède ou suit les fluctuations de température.

Le GIEC justifie son hypothèse en se référant à l’équation semi-empirique de (Myhre et al. 1998). Elle lie le forcing radiatif (et donc la température) à la teneur en CO₂. Il s’agit d’une corrélation, qui ne donne évidemment pas la direction du lien de causalité.

Nous avons développé un second modèle pour lier la concentration atmosphérique en CO₂ à la température de surface des océans. Il est basé sur les équilibres de Henry et van t’Hoff ; il permet de retrouver la formule de Myhre, qui trouve donc ainsi une justification théorique.
Notre modèle tient également compte des équilibres entre ions (bi)carbonates et CO₂ dissous au sein de l’océan (« pompe chimique » réduisant la quantité de CO₂ dissous dans l’océan, ou effet Suess).

Notre analyse des données expérimentales révèle d’un point de vue statistique que

l’activité solaire moyennée est significativement la cause de la température de surface des océans.
la température de surface des océans est significativement la cause de la concentration du CO₂ atmosphérique, et qu’il y a une causalité moins marquée en sens inverse. Ceci s’interprète simplement comme correspondant à un retour à l’équilibre des échanges de matière et de chaleur entre océan et atmosphère.

Ces résultats discréditent la thèse de l’effet de serre atmosphérique (qui impliquerait un lien causal unique et exclusivement unidirectionnel allant de la concentration en CO₂ atmosphérique vers la température).

1.5 Méthodologie

Dans la présente étude, les séries temporelles de divers « proxies » de température et d’activité solaire ont fait l’objet de différents traitements : analyse statistique de régression non linéaire, analyse harmonique par spectre de puissance, analyses de corrélation et de corrélation croisée, analyse de résidus, analyse de causalité de Granger, afin de confirmer ou infirmer ce que la littérature nous a appris, avant de procéder à la construction d’un modèle climatique, certes élémentaire mais satisfaisant pour expliquer les résultats obtenus.

Les analyses ont été effectuées au moyen de scripts écrits dans les langages opensource R et Python. R est un langage fort spécialisé pour les analyses de données, mais les calculs de régression multiple non linéaires présentaient souvent des problèmes de convergence dans cet environnement et ont par conséquent été faites en Python qui s’est avéré mieux adapté à cette tâche.

On ne saurait trop recommander l’ouvrage de (Hyndman et Athanasopoulos 2018) qui reprend d’excellents principes pour l’étude de séries temporelles, avec de nombreux exemples en langage R.

De nombreux acronymes sont utilisés dans les synthèses des calculs de régression. La Table 1.1 et la Table 1.2 en reprennent quelques uns.

La précision globale d’ajustement d’un modèle de régression est mesurée suivant différentes formules basées sur les erreurs de modélisation de chaque observation. Les acronymes des principales formules et leurs noms sont repris dans la Table 1.1.

Table 1.1: Acronymes et noms des erreurs globales.
Acronyme	Nom
MAE (*)	Mean Absolute Error
RMSE (*)	Root Mean Square Error
MAPE (**)	Mean Absolute Percentage Error
sMAPE (**)	Symmetric MAPE
MPE (***)	Mean Percentage Error
MASE (***)	Mean Absolute Scaled Error
(*)	Scale dependent errors
(**)	Percentage errors
(***)	Scaled errors

Pour de plus amples informations, voir (Hyndman et Athanasopoulos 2018, chap. 3.4)

Lorsqu’il y a plusieurs variables indépendantes susceptibles d’être utilisées dans la régression d’une variable dépendante, les modèles correspondants à chaque choix ou combinaison de choix sont triés sur base de leurs capacités prédictives que l’on peut évaluer selon différents critères.

Lorsqu’il y a peu de variables indépendantes, toutes les combinaisons possibles peuvent être testées, et la meilleure combinaison peut être objectivement sélectionnée.

Les acronymes et les noms des principaux critères sont repris dans la table Table 1.2.

Table 1.2: Acronymes et noms des principaux critères de capacité prédictive
Acronyme	Nom
CV	Cross-validation
AIC	Akaike’s Information Criterion
AICc	Corrected Akaike’s Information Criterion
BIC (ou SBIC ou SC)	Schwarz’s Bayesian Information Criterion
AdjR2	Adjusted R2

Un modèle sera d’autant meilleur que ses critères CV, AIC, AICc, BIC seront petits et que son critère AdjR2 est élevé. Pour de plus amples informations, voir (Hyndman et Athanasopoulos 2018, chap. 5.5)